3.3 Lösning 7a

Ursäkta att det inte finns någon lösning här. Jag har inte hunnit att skriva den än.

Jag ska göra det så fort jag hinner.

Hälsningar

Taifun

\[\begin{array}{rcl} f(x) & = & 2\,x^5 - 5\,x^4 - 10\,x^3 + 20\,x^2 + 40\,x + 23 \\ f'(x) & = & 10\,x^4 - 20\,x^3 - 30\,x^2 + 40\,x + 40 \\ f''(x) & = & 40\,x^3 - 60\,x^2 - 60\,x + 40 \\ f'''(x) & = & 120\,x^2 - 120\,x - 60 \end{array}\]

Digital beräkning av derivatans nollställen:

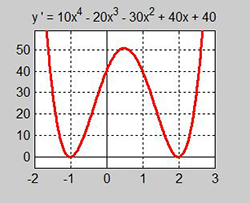
\[ f'(x) \, = \, 10\,x^4 - 20\,x^3 - 30\,x^2 + 40\,x + 40 \, = \, 0 \]

a)   Vi tar fram först närmevärden för lösningarna genom att rita grafen till derivatfunktionen \( \, y' \, = \, f'(x) \, \):

Dessa närmevärde används sedan i EQUATION SOLVER för att få lösningen mera exakt.