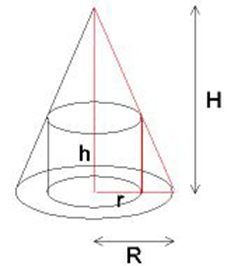
3.5 Övningar till Extremvärdesproblem

<< Förra avsnitt

Genomgång

Övningar

Diagnosprov kap 3 Anv. av deriv.

Lösningar till diagnosprov kap 3

E-övningar: 1-5

Övning 1

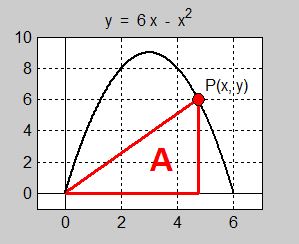
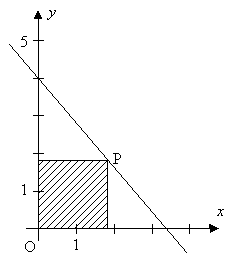
I figuren till höger rör sig punkten \( \, P \, \) på den räta linje vars ekvation är:

\[ y = -\,{6 \over 5}\,x + 4 \]

Vilken position av \( \, P \, (x, \, y) \, \) ger maximal area till den skuggade rektangeln?

a) Vad är problemets bivillkor?

b) Ställ upp problemets målfunktion som en funktion av endast en variabel.

c) Bestäm koordinaterna till \( \, P \, \) så att rektangelns area blir maximal.

d) Beräkna rektangelns maximala area.

Svar 1a

Svar 1b

Lösning 1b

Svar 1c

Lösning 1c

Svar 1d

Lösning 1d

Övning 2

En rektangel har omkretsen \( \, 12 \, {\rm cm} \, \). Maximera rektangelns area.

a) Formulera problemets bivillkor.

b) Ange problemets målfunktion.

c) Bestäm sidorna \( \, x \, \) och \( \, y \, \) så att rektangelns area blir maximal.

d) Vad blir rektangelns maximala area?

Svar 2a

Lösning 2a

Svar 2b

Lösning 2b

Svar 2c

Lösning 2c

Svar 2d

Övning 3

En rektangels area är \( \, 25 \, {\rm cm}^2 \, \). Minimera rektangelns omkrets.

a) Formulera problemets bivillkor.

b) Ange problemets målfunktion.

c) Bestäm sidorna \( \, x \, \) och \( \, y \, \) så att rektangelns omkrets blir minimal.

d) Vad blir rektangelns minimala omkrets?

Svar 3a

Lösning 3a

Svar 3b

Lösning 3b

Svar 3c

Lösning 3c

Svar 3d

Övning 4

En rätvinklig triangel är inbunden i en parabel enligt figuren:

Parabeln är definierad genom:

\[ y \, = \, 6 \, x \, - \, x^2 \qquad {\rm med} \qquad 0 \, \leq \, x \, \leq \, 6 \]

Punkten \( \, P\,(x,\,y) \, \) rör sig på parabeln.

Vilken position av \( \, P \, \) ger triangeln största möjliga arean \( \, A \, \)?

a) Ange problemets bivillkor.

b) Ställ upp problemets målfunktion som en funktion \( \, A(x) \, \).

c) Bestäm koordinaterna till \( \, P \, \) så att triangelns area blir maximal.

d) Beräkna triangelns maximala area.

Svar 4a

Svar 4b

Lösning 4b

Svar 4c

Lösning 4c

Svar 4d

Lösning 4d

Övning 5

Navigeringsmeny

Logga in

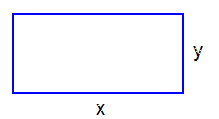
En fårherde vill samla sina får vid en mur i ett rektangulärt stängsel.

Hon/han avgränsar stängslet med ett rep och pinnar i marken enligt

figuren. Repet är \( \, 9 \; {\rm m} \, \) långt (rött).

Beteckna rektangelns kortare sida med \( \, x \). Hur ska fårherden välja

stängslets mått för att få den störst möjliga arean \( \, A \, \) för sina får?

a) Skriv \( \, A \, \) som en funktion av \( \, x \), problemets målfunktion \( \, A(x) \, \).

b) Ange målfunktionens definitionsmängd.

c) Bestäm \( \, x \, \) så att stängslets area blir maximal.

d) Beräkna stängslets maximala area.

e) Har problemet ett bivillkor? Om ja, ange det.

Svar 5a

Lösning 5a

Svar 5b

Svar 5c

Lösning 5c

Svar 5d

Lösning 5d

Svar 5e

Lösning 5e

</div>

C-övningar: 6-7

Övning 6

Du ska bygga en öppen låda av en kvadratisk kartong på \( \, 10 \times 10 \; {\rm dm} \, \).

Det gör du genom att skära ut små kvadrater av längden \( \, x \, \) från karton-

gens fyra hörn enligt figuren.

Hur ska du välja \( \, x \, \) för att få den största möjliga volymen \( \, V \, \) för din

öppna låda?

a) Inför en ny beteckning och ange problemets bivillkor, se Lösning 5 e).

b) Ställ upp problemets målfunktion \( \, V(x) \, \).

c) Ange målfunktionens definitionsmängd.

d) Bestäm \( \, x \, \) så att lådans volym \( \, V(x) \, \) blir maximal.

e) Beräkna lådans maximala volym.

f) Vilka mått har lådan med maximal volym?

Ange dina svar med två decimaler.

Svar 6a

Lösning 6a

Svar 6b

Lösning 6b

Svar 6c

Lösning 6c

Svar 6d

Lösning 6d

Svar 6e

Lösning 6e

Svar 6f

Lösning 6f

Övning 7

SJ har \( \, 20\,000 \, \) passagerare per månad på en viss bansträcka med ett biljettpris på \( \, 200 \, \) kr.

En marknadsundersökning visar att varje höjning av biljettpriset med \( \, 1 \, \) kr skulle medföra

en förlust av \( \, 80 \, \) passagerare per månad.

Vilken biljettprishöjning kommer att maximera intäkten per månad?

a) Ange problemets bivillkor om

\( \qquad\;\; x \, = \, \) Den planerade prishöjningen i kr.

\( \qquad\;\; y \, = \, \) Antalet passagerare per månad efter prishöjningen \( \, x \, \).

b) Ställ upp problemets målfunktion \( \, I(x) \, \) för SJ:s intäkt per månad.

c) Bestäm \( \, x \, \) så att intäkten \( \, I(x) \, \) blir så stor som möjligt.

d) Beräkna den maximala intäkten efter en biljettprishöjning på \( \, x \, \) kr.

e) För vilka prishöjningar kommer det inte längre att löna sig att höja biljettpriset?

Svar 7a

Lösning 7a

Svar 7b

Lösning 7b

Svar 7c

Lösning 7c

Svar 7d

Lösning 7d

Svar 7e

Lösning 7e

A-övningar: 8-9

Övning 8

En cylinder är placerad inuti en kon enligt figuren. Kons mått är givna:

\[ R \, = \, {\rm Radien\;till\;kons\;bascirkel\;} \, = \, 15 \; {\rm cm} \]

\[ H \, = \, {\rm Kons\;höjd\;} \, = \, 30 \; {\rm cm} \]

Vilka mått på cylindern maximerar dess volym \( \, V \, \)?

a) Formulera problemets bivillkor. Använd den röda triangeln i figuren.

b) Ställ upp problemets målfunktion \( \, V(r) \, \) där \( r = \) cylinderns radie.

c) Bestäm cylinderns radie \( \, r \, \) och höjd \( \, h \, \) så att volymen blir maximal.

d) Beräkna cylinderns maximala volym.

e) Vilket förhållande råder mellan cylinderns radie \( \, r \, \) och dess höjd \( \, h \, \)

när volymen maximeras?

Svar 8a

Lösning 8a

Svar 8b

Lösning 8b

Svar 8c

Lösning 8c

Svar 8d

Lösning 8d

Svar 8e

Lösning 8e

Övning 9

För att producera en cylinderformad konservburk har man en viss mängd \( \, A \, \)

plåt till förfogande (efter spill). Dvs cylinderns begränsningsarea \( \, = \, A \; {\rm cm}^2 \, \).

I genomgången, Exempel 3 Konservburk, löstes denna uppgift för \( \, A = 500 \).

Här ska du lösa den generellt för en given konstant \( \, A \, \).

Vilka mått på konserven maximerar volymen?

a) Formulera problemets bivillkor.

b) Ställ upp problemets målfunktion.

c) Bestäm cylinderns radie så att burkens volym blir maximal.

d) Bestäm cylinderns höjd när burkens volym maximeras och visa:

För en cylinder med maximal volym gäller för radien \( \, r \, \) och höjden \( \, h \, \):

\[ 2 \; r \; = \; h \]

Svar 9a

Lösning 9a

Svar 9b

Lösning 9b

Svar 9c

Lösning 9c

Svar 9d

Lösning 9d

3.5 Övningar till Extremvärdesproblem

Övning 1

Övning 2

Övning 3

Övning 4

Övning 5

Navigeringsmeny

Personliga verktyg

Matematik 3c

Sök

Övning 6

Övning 7

Övning 8

Övning 9