2.7 Numerisk derivering
| Teori | Övningar |
Innehåll
Varför numerisk derivering?
Numerisk derivering är en metod för approximativ (ungefärlig, nära men inte exakt) beräkning av derivatan. Med hjälp av numeriska deriveringsformler beräknas ett nämevärde för derivatan.
Frågan uppstår: varför ska vi ta fram ett nämevärde när vi kan få derivatans exakta värde med hjälp av de deriveringsregler som vi sammanställde i en tabell i förra avsnitt? Svaret är: Ibland eller t.o.m. ofta kan vi inte göra det, vilket blir klarare om vi tittar på den numeriska deriveringens användningsområden.
Numerisk derivering används i följande situationer:
- 1) När vi ska derivera t.ex. följande funktion konstaterar vi att den inte matchar med någon funktionstyp i vår deriveringstabell. Den kan inte deriveras med någon av de deriveringsregler vi känner till hittills:
- \[ f(x) = {1 \over x + 1} \]
- Först i Matte D-kursen lär man sig den s.k. kvotregeln med vars hjälp en kvot (resultat av en division) av två funktioner kan deriveras.
- Ett annat exempel är \( f(x) = \ln x\, \) som inte heller matchar mot någon funktionstyp i vår deriveringstabell och vars numerisk derivering visas i Exempel 2 längre fram.
- 2) När vi har en funktion vars derivata blir så komlicerad att det tar mer tid att ställa upp den än att genomföra numerisk derivering. Exempel:
- \[ f(x) = {\sin\,3\,x \over 4\,\cos\,x} \]
- \[ f\,'(x) = {12\,\cos\,3\,x \cdot \cos\,x \,+\, 4\,\sin\,3\,x \cdot \sin\,x \over 16\,\cos^2\,x} \]
- För det första är det inte enkelt att ställa upp \( f\,'(x) \). Även detta görs med kvotregeln som vi inte känner till.
- För det andra ser man att det är väsentligt enklare att beräkna t.ex. \( f(2)\, \) än \( f\,'(2) \). I de numeriska deriveringsformlerna ingår nämligen endast beräkningar av \( f(x)\, \), inte av \( f\,'(x) \).
- 3) När vi ska derivera en funktion som saknar algebraisk formel och är endast given i tabellform, dvs numeriskt. Pga avsaknaden av en formel finns det ingen annan möjlighet att derivera den än numerisk derivering. Ett exempel:

- Sådana funktioner förekommer ofta som resultat av mätdata utan någon formel. Ändå uppfyller de definitionen på en funktion, nämligen att vara en
- "Regel som tilldelar varje \( x\, \)-värde endast ett \( y\, \)-värde."
Det finns en uppsjö av numeriska deriveringsformler. Vi behandlar i detta avsnitt de tre enklaste:
- Framåtdifferenskvoten
- Bakåtdifferenskvoten
- Centrala differenskvoten
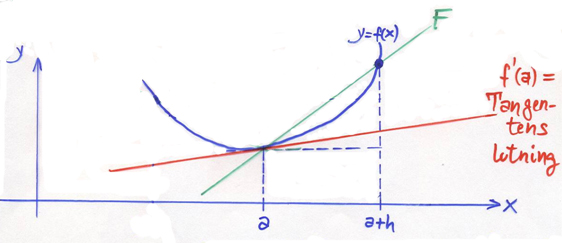
Framåtdifferenskvoten
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Framåtdifferenskvoten:
- \[ f\,'(a) \qquad \approx \qquad {f(a + h) \, - \, f(a) \over h} \qquad {\color{White} x} \]
- Tangentens lutning \( {\color{White} x} \approx {\color{White} x} \) Sekanten F:s lutning
\( h\, \) kallas steglängden. Approximationen är desto bättre ju mindre steglängden är.
Exempel 1
Följande funktion \( f(x)\, \) är given i tabellform:
\( x\, \) \( f(x)\, \) \( 0,5\, \) \( 1,79744\, \) \( 0,6\, \) \( 2,04424\, \) \( 0,7\, \) \( 2,32751\, \)
Beräkna funktionens derivata i \( x = 0,6\, \) dvs \( f\,'(0,6) \) med framåtdifferenskvoten.
Lösning:
Steglängden är given i tabellen\[ h = 0,1\, \]
\( f\,'(0,6) = {f(0,6 + 0,1) - f(0,6) \over 0,1} = {f(0,7) - f(0,6) \over 0,1} = {2,32751 - 2,04424 \over 0,1} = {0,28327 \over 0,1} = 2,8327 \)
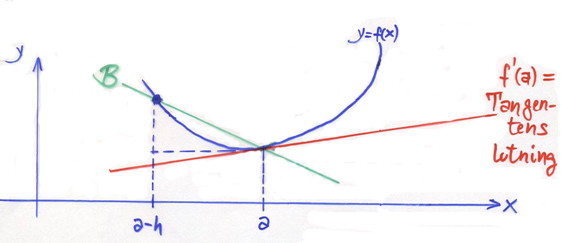
Bakåtdifferenskvoten
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Bakåtdifferenskvoten:
- Tangentens lutning \( \; = \; f\,'(a) \quad \approx \quad {f(a) \, - \, f(a-h) \over h} \; = \; \) Sekanten B:s lutning
Även här gäller att approximationen är desto bättre ju mindre steglängden \( h\, \) är.
Exempel 2
Givet:
- Funktionen \( f(x) = \ln x\, \)
- Steglängden \( h = 0,01\, \)
Sökt:
- Funktionens derivata i \( x = 1,8\, \) dvs \( f\,'(1,8) \) med bakåtdifferenskvoten .
Lösning\[ f\,'(1,8) \approx {f(1,8) - f(1,8 - 0,01) \over 0,01} = {f(1,8) - f(1,79) \over 0,01} = {\ln(1,8) - \ln(1,79) \over 0,01} = 0,5571 \]
Det exakta värdet avrundat till 4 decimaler är \( f\,'(1,8) = 0,5556\, \).
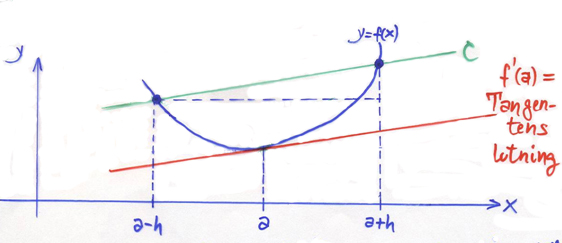
Centrala differenskvoten
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Centrala differenskvoten:
- Tangentens lutning \( \; = \; f\,'(a) \quad \approx \quad {f(a + h) \, - \, f(a-h) \over 2\,h} \; = \; \) Sekanten C:s lutning
Approximationen är desto bättre ju mindre \( h\, \) är.
Exempel 3
Givet:
- Funktionen \( f(x) = x\,^2 \)
- Steglängden \( h = 0,5\, \)
Sökt:
- Funktionens derivata i \( x = 1\, \) dvs \( f\,'(1) \) med centrala differenskvoten .
Lösning\[ f\,'(1) \approx {f(1 + 0,5) - f(1 - 0,5) \over 2\cdot 0,5} = {f(1,5) - f(0,5) \over 2\cdot 0,5} = {1,5^2 - 0,5^2 \over 1} = 2 \]
Funktionens derivata är \( f\,'(x) = 2\,x \) och därmed det exakta värdet \( f\,'(1) = 2 \cdot 1 = 2 \).
Är det en slump att den numeriska deriveringen ger exakt värde, fast steglängden är relativt stor?
Svaret är nej: Den centrala differenskvoten deriverar alla 2:a gradsfunktioner (och förstås även alla 1:a gradsfunktioner) exakt oberoende av steglängden. Här följer beviset:
Sats:
- Den centrala differenskvoten ger den exakta derivatan till alla 2:a gradsfunktioner oberoende av steglängden.
- Om \( f(x) \; = \; x^2 \)
- då \( {f(x + h) \, - \, f(x-h) \over 2\,h} \; = \; 2\,x \)
Bevis\[ {f(x + h) - f(x-h) \over 2\,h} = {(x+h)^2 - (x-h)^2 \over 2\,h} = {(x^2 + 2\,x\,h + h^2) - (x^2 - 2\,x\,h + h^2) \over 2\,h} = \]
\( = {x^2 + 2\,x\,h + h^2 - x^2 + 2\,x\,h - h^2 \over 2\,h} = {4\,x\,h \over 2\,h} = 2\,x = f\,'(x) \)
Det räcker att bevisa satsen för \( f(x) = x^2\, \) som an slags representant för alla 2:a gradsfunktioner, eftersom \( x^2\, \) är den avgörande termen för 2:a gradsfunktioner. Självfallet går det att bevisa satsen även för \( f(x) = a\,x^2 + b\,x + c \). Det tar bara lite längre att räkna. Resultatet är det samma: Den centrala differenskvoten deriverar 2:a gradsfunktionerna exakt. Att detta är oberoende av steglängden visas i beviset ovan genom att \( h\, \) förkortas bort i slutet.
Copyright © 2010-2012 Taifun Alishenas. All Rights Reserved.