3.4 Kurvkonstruktioner
| <-- Förra avsnitt | Teori | Övningar | --> Nästa avsnitt |
Innehåll
Fortfarande förutsätts att alla funktioner \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) vi behandlar här är kontinuerliga i alla punkter av det betraktade området.
Globala maxima och minima
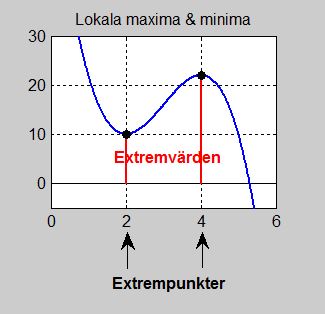
I avsnittet om Lokala maxima och minima hade vi tittat på sådana punkter som hade maximala och minimala \( \, y\)-värden i sin närmaste omgivning, därför "lokala", se bilden till höger.
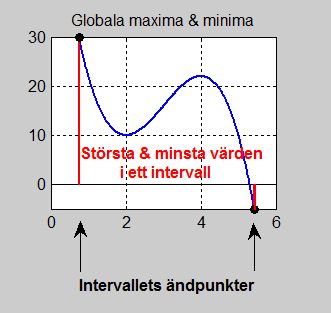
I detta avsnitt ska vi betrakta sådana punkter som har största och minsta \( \, y\)-värden i funktionens hela definitionsområde som i regel är ett intervall, därför "globala", se bilden till vänster.
 |
Globala maxima och minima är en funktions största och minsta värden
globalt dvs i ett intervall, närmare bestämt: Med globala maxima och globala minima menas punkter (•) som har största resp. minsta \( \, y\)-värden i funktionens hela definitionsområde, se bilden till vänster. Globala maxima och minima antas antingen i de lokala maxima och minima eller i intervallets ändpunkter. På bilden till vänster har funktionen i intervallet \( \, 0 \neq x \neq 6 \, \) största värdet \( \, 30 \, \) och minsta värdet \( \, -5 \, \) (OBS! \( \, y\)-värden). Globala maxima och minima har i regel ingenting att göra med derivatan. Annars än att de sammanfaller med funktionens lokala extrema. |
 |
Det finns två alternativa metoder att göra det, den ena använder andraderivatan, den andra genomför ett teckenstudium. Vi ställer upp regler och löser exempel för båda metoderna.
