1.3 Fördjupning till Rationella uttryck
| Repetition: Bråkräkning | Genomgång | Övningar | Fördjupning | Nästa avsnitt --> |
Lektion 7 Rationella uttryck: Fördjupning
Varför är division med 0 inte definierad?
Om du matar in i din miniräknare:
- \[ 1 \, / \, 0 \]
kommer du att få ERROR på displayen. Räknaren kan inte genomföra denna operation.
Division med 0 är den viktigaste "förbjudna" operationen i matematiken.
Både i bråktal och i uttryck får nämnaren inte bli \( \, 0\, \) eftersom division med \( \, 0\, \) inte är definierad.
Men vad beror det på att man inte kan dividera med \( \, 0\, \)?
När vi besvarar denna fråga kommer vi att inse att det inte är ett formellt förbud utan en praktisk omöjlighet.
Praktisk förklaring
Matar in i din miniräknare:
- \[ 1 \, / \, 0,1 \qquad 1 \, / \, 0,01 \qquad 1 \, / \, 0,001 \qquad \ldots \]
Anteckna resultaten. Fortsätt med att låta de små tal som du delar med, bli mindre och mindre:
|
\( \qquad\qquad\qquad \) |
Tabellen ovan visar: Ju mindre \( x\, \) blir desto större blir \( \displaystyle {1 \over x} \). I gränsfallet \( x = 0\, \) blir \( \displaystyle {1 \over x} \) oändligt stort.
Man säger: \( \displaystyle {1 \over x} \) går mot oändligheten när \( \, x\, \) går mot \( \, 0\, \) och skriver: \( \, \displaystyle {1 \over x} \to \infty \, \) när \( \, x \, \to \, 0 \).
\( \infty \) är symbolen för oändligheten. Det är omöjligt att ange \( \infty \) som ett tal som man kan räkna med.
Vilket tal man än anger så kan man alltid göra \( \, + \, 1 \, \) och få ett större tal. Det tar aldrig slut.
Slutsatser: \( \displaystyle \quad {1 \over 0} \) är inget tal och därmed inte definierat.
Slutsatser: \( \quad \)Det är matematiskt inte korrekt att skriva \( \displaystyle \, {1 \over x} = \infty \, \).
Teoretisk förklaring
Vad betyder \( \, 12 / 4 \, \)?
- \[ 12 / 4 = {\color{Red} x} \quad {\rm betyder: \quad Att\;hitta\;ett\;tal\;}{\color{Red} x}\; {\rm så\;att\;} {\color{Red} x} \cdot 4 = 12 \]
Uppenbarligen är detta tal \( \quad {\color{Red} {x = 3}} \quad \) därför att \( \, {\color{Red} 3} \cdot 4 = 12 \).
Nu ersätter vi \( \, 4 \, \) med \( \, 0 \, \):
Vad betyder \( \, 12 / 0 \, \)?
- \[ 12 / 0 = {\color{Red} x} \quad {\rm betyder: \quad Att\;hitta\;ett\;tal\;}{\color{Red} x}\; {\rm så\;att\;} {\color{Red} x} \cdot 0 = 12 \]
Men det finns inget sådant tal \( {\color{Red} x} \) därför att \( \quad {\color{Red} x} \cdot 0 = 0 \quad \neq 12 \, \).
Ett annat sätt att förklara omöjligheten av division med \( \, 0 \, \) är att tolka divisionen som en upprepad subtraktion.
Operationen \( \, 12 / 4 \, \) kan tolkas som:
- \[ 12 \; \underbrace{- \, 4 \, - \, 4 \, - \, 4}_{3\;\times} \; = \; 0 \qquad {\rm Därför:} \qquad 12 \, / \, 4 \; = \; 3\,, \;\; {\rm rest\;\;} 0 \]
Nu ersätter vi \( \, 4 \, \) med \( \, 0 \, \).
Operationen \( \, 12 / 0 \, \) kan tolkas som:
- \[ 12 \; - \, 0 \, - \, 0 \, - \, \ldots - \, 0 \; = \; 12 \]
Man kan alltså dra av hur många nollor som helst från \( \, 12 \, \) utan att det blir mindre: En oändlig process ger inget resultat.
Slutsats: Division med \( 0 \,\) är omöjligt att genomföra.
Rationella funktioner
Ett bra sätt att studera rationella uttryck är att bilda funktioner med dem genom att tilldela dem en annan variabel, t.ex. \( y\, \).
Fördelen med funktioner är är att man kan visualisera dem med grafer.
Exempel 1
Det enklast tänkbara exemplet på ett rationellt uttryck är \( \quad \displaystyle{\frac{1}{x}} \quad \) därför att det är en kvot mellan polynomet \( 1\, \) (av graden 0) och polynomet \( x\, \) (av graden 1).
En rationell funktion är alltså kvoten mellan två polynom som tilldelas en variabel \( y\, \).
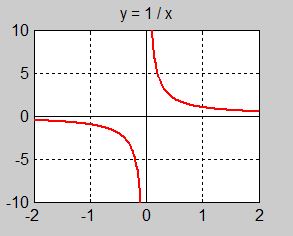
- Funktionen är diskontinuerlig i \( \; {\color{Red} {x = 0}} \).
Den väsentliga skillnaden mellan denna graf och polynomfunktioners graf är att den här har två skilda grenar, medan en polynomfunktions graf har ett sammanhängande förlopp. Uttryckt i matematiska termer: en polynomfunktion är alltid kontinuerlig. Ett polynoms graf kan ritas utan att man lyfter pennan från papperet.
I grafen ovan måste vid \( x = 0\, \) pennan lyftas för att gå från grafens ena gren till den andra. Dvs grafen är inte sammanhängande i \( x = 0\, \). Man säger att funktionen är icke-kontinuerlig eller diskontinuerlig i \( x = 0\, \).
Anledningen till denna diskontinuitet är att \( \; y = \) \( \displaystyle {1 \over x} \; \) inte är definierad för \( x = 0\, \). När \( x \, \) närmar sig \( 0\, \) går \( y\, \) mot oändligheten, vilket tydligt framgår av grafen. Man måste undanta \( x = 0\, \) från funktionens definitionsmängd:
Den rationella funktionen \( y = \) \( \displaystyle {1 \over x} \) är definierad för alla \( x\,\neq\,0 \).
Icke-definierbarheten och diskontinuiteten för vissa \( \, x \, \) är något typiskt för alla rationella funktioner och det är det som skiljer dem från polynomfunktioner som är definierade och kontinuerliga för alla \( x\, \).
Diskontinuiteten för vissa \( \, x\, \) innebär att det är bara några isolerade \( \, x\)-värden för vilka en rationell funktion kan vara diskontinuerlig. Antalet sådana \(\,x\)-värden kan hos rationella funktioner vara \( \, 0,\, 1,\, 2,\, \ldots \). Antalet \( \, 0\, \) innebär att det även finns rationella funktioner som inte har några diskontinuiteter, dvs de är kontinuerliga för alla \( \, x\, \) precis som vanliga polynom.
Exempel 2
Ett exempel på rationella funktioner utan diskontinuiteter, s.k. "snälla" rationella funktioner är:
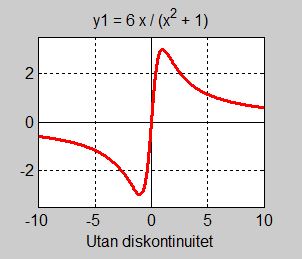
Nämnaren kan inte faktoriseras (inom reella talen) dvs \( x^2 + 1\, \) har inte några reella nollställen. Det i sin tur beror på att ekvationen \( x^2 + 1 = 0\, \) saknar reell lösning därför att den ger \( x^2 = -1\, \) och roten ur \( -1\, \) inte är ett reellt tal. \( \quad \Rightarrow \quad \) Den rationella funktionen \( \, y_1 \, \) är kontinuerlig för alla \( \, x \), vilket även bekräftas av grafen.
En liten ändring endast i ett tecken i nämnaren, från \( \, x^2 \, \bf{{\color{Red} +}} \, 1 \, \) till \( \, x^2 \, \bf{{\color{Red} -}} \, 1 \, \) resulterar i en annan funktion med ett helt annorlunda beteende:
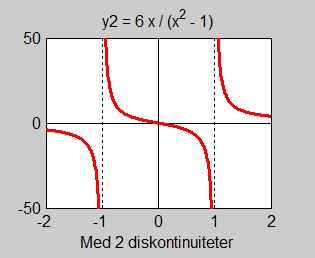
Nämnaren kan faktoriseras och har nollställena \( \, x = 1 \, \) och \( \, x = -1\, \). \( \quad \Rightarrow \quad \) Den rationella funktionen \( \, y_2 \, \) har två diskontinuiteter: \( \, x = 1 \, \) och \( \, x = -1\, \).
Med andra ord: Den rationella funktionen \( \, y_2 \, \) är definierad och kontinuerlig för alla \( \ x \, \neq \, 1\) och \( \, x \, \neq \, -1 \, \).
Som grafen visar är \( \, y_2\):s kurva uppdelad i tre grenar och har två ställen där den inte är sammanhängande (inte kontinuerlig). När \( x\, \) närmar sig \( -1\, \) eller \( 1\, \) går \(y_2\,\) mot oändligheten.
Exemplet visar att det som är väsentligt för rationella funktioner och därmed för rationella uttryck, är om nämnaren låter sig faktorisera eller ej, dvs om polynomet i nämnaren har några nollställen och, om det är fallet, vilka de är. De utgör den rationella funktionens diskontinuiteter.
Det finns två typer av diskontinuiteter:
Hävbara och icke-hävbara diskontinuiteter
Vi har hittills använt bråktalens räkneregler för att räkna med rationella uttryck utan att stöta på några hinder. Denna analogi har sina gränser: Rationella uttryck är ändå inga bråktal. De är komplexare. Därför är det inte förvånansvärt att de har egenskaper som inte längre kan jämföras med bråktal. En av dessa visar sig när man förkortar dem efter faktorisering av täljaren och nämnaren.
Exempel 3
Den första diskontinuiteten \( \, x = -3 \, \) som vi lyckades få bort genom förkortning av faktorn \( \, x + 3 \), kallas för en hävbar diskontinuitet, medan den andra diskontinuiteten \( \, x = 3 \, \) som är kvar i form av faktorn \( \, x - 3 \, \) i nämnaren, är en icke-hävbar diskontinuitet.
Efter faktorisering av täljaren och nämnaren samt förkortning med faktorn \( \, (x+3) \, \) förenklas det rationella uttrycket väsentligt. Men denna förkortning är endast korrekt om \( \, x \not= -3 \) eftersom förkortning med \( \, (x+3) \,\) innebär division med \( \, 0\,\) om \( \, x = -3\, \).
OBS! Se upp för division med \( \, 0 \,\) i uttryck, för den är oftast gömd. Man kan råka ut för den utan att märka. Läs vad som kan hända om man dividerar med \( \, 0 \,\) i uttryck.
Det sista likhetstecknet mellan de rationella uttrycken i exempel 3 gäller endast under förutsättningen \( \, x \not= -3 \). Det enklare uttrycket är identiskt med det ursprungliga inte för alla \( \, x \, \) utan för alla utom för \( \, x = -3\, \).
Det blir ännu tydligare när vi skriver om de rationella uttrycken som rationella funktioner. Det uppstår nämligen två olika funktioner:
| \(\begin{align} f(x) & = {2\,x^2 + 6\,x \over x^2 - 9} = {2\,x\,{\color{Red} {(x + 3)}} \over {\color{Red} {(x + 3)}}\,(x - 3)} \\ \\ g(x) & = {2\,x \over x - 3}\end{align} \) | \( \qquad \) | 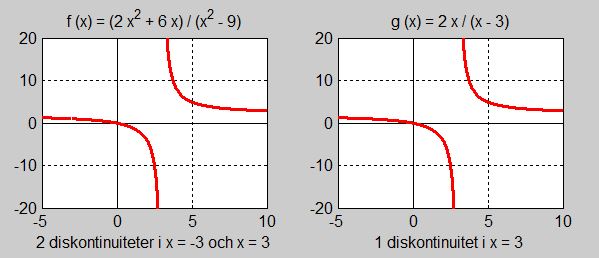 |
Dessa funktioner är olika därför att deras definitionsmängder är olika. Medan \( \, f(x)\, \) är definierad för alla \( \ x \, \neq \, -3\) och \( \, x \, \neq \, 3 \, \), är \( \, g(x)\, \) definierad för alla \( \ x \, \neq \, 3\).
OBS! Funktionernas grafer lurar oss. Med blotta ögat ser man knappast någon skillnad mellan \( \, f(x) \, \) och \( \, g(x) \, \). I själva verket har \( \, f(x)\, \) ett "hål" eller en "lucka" i \( \, x = -3 \), är inte definierad och har en diskontinuitet där. Den "hoppar" över \( \, x = -3 \, \) så att säga. Men pga att denna diskontinuitet är hävbar går funktionen inte mot oändligheten kring den.
Kontinuerlig fortsättning
Hävbara diskontinuiteter är "snälla" och kan "repareras". En ny funktion kan definieras som inte längre har den ursprungliga funktionens hävbara diskontinuiteter, men är annars identisk med den. En sådan funktion kallas den kontinuerliga fortsättningen av den ursprungliga.
I det här fallet skulle man kunna t.ex. komplettera funktionen \( \, f(x)\, \):s definition med ett värde för \( \, x = -3 \, \) som gör att den nya funktionen blir kontinuerlig mot sin omgivning. Hur får man fram detta värde? Man gör det genom att beräkna \( \, g(-3) \):
- \[ g(-3) = {2 \cdot (-3) \over -3 - 3} = {-6 \over -6} = 1 \]
Värdet \( 1\, \) överensstämmer med \( \, f(x)\):s gränsvärde när \( \, x\, \) närmar sig \( -3\, \). Dvs \( \, f(x)\, \) går mot \( \, 1\, \) när \( \, x\, \) går mot \( \, -3\, \) både från vänster och höger.
Då är det möjligt att definiera den nya funktionen som en lite modifierad version av \( \, f(x) \). Modifikationen består i att lägga till värdet \( \, 1 \, \) i den nya funktionen för \( \, x = -3 \, \) så att den blir både definierad och kontinuerlig för \( \, x = -3 \). För alla andra \( \, x \, \) är den identisk med \( f(x)\, \).
Så här kan man definiera den nya funktionen:
- \[ \hat{f}(x) \, = \, \begin{cases} \displaystyle {2\,x^2 + 6\,x \over x^2 - 9} & \mbox{om } x \neq -3 \\ \\ 1 & \mbox{om } x = -3 \end{cases}\]
Denna definition är uppdelad i två olika fall: För alla \( x \neq -3\, \) definieras funktionen \( \, \hat{f}(x) \, \) enligt det rationella uttrycket för \( f(x)\, \), medan för \( x = -3\, \) har den värdet \( 1\, \).
\(\hat{f}(x) \, \) är den kontinuerliga fortsättningen av \( \ f(x) \) och är helt och hållet identisk med den förkortade form som vi hade fått tidigare:
- \[ \hat{f}(x) \, = \, g(x) \, = \, {2 \, x \over x - 3} \]
I praktiskt beräkningssammanhang och när man ritar grafen föredrar man förstås denna enkla form. Nackdelen med den är bara att den inte längre innehåller något spår av den ursprungliga funktionen \( f(x)\, \), att den gömmer sina rötter. Man ser inte direkt varifrån den kommer, att den är en kontinuerlig fortsättning av \( f(x)\, \).
Den andra faktorn \( (x-3)\, \) både i \( \,f(x)\):s och \( \, \hat{f}(x)\):s nämnare som inte kan förkortas ger upphov till den andra diskontinuiteten \( \, x = 3 \). När \( \, x\, \) går mot \( \, 3\, \) går \( \, f(x)\, \) inte mot ett ändligt värde utan mot oändligheten. Därför är diskontinuiteten i \( x = 3\, \) kvar och synlig i graferna till både \( \, f(x)\, \) och \( \, \hat{f}(x) \, \). Den är, till skillnad från den första, en icke-hävbar diskontinuitet och kan inte "repareras" på något sätt. Denna "allvarliga" diskontinuitet finns även kvar i den kontinuerliga fortsättningen \( \, \hat{f}(x) \). Så \( \, \hat{f}(x) \, \) har en diskontinuitet kvar medan \( f(x)\, \) hade två diskontinuiteter.
Copyright © 2011-2015 Taifun Alishenas. All Rights Reserved.
