3.1 Växande och avtagande
| Teori | Övningar | --> Nästa avsnitt |
Lektion 28 Växande och avtagande I
Lektion 29 Växande och avtagande II
I detta kapitel kommer vi att använda derivatan som ett verktyg för att få information om själva funktionen.
I det här avsnittet gör vi det för att få reda på om funktionen växer eller avtar. För just detta ändamål räcker det till att titta på derivatans tecken.
Förutsättning i hela det här avsnittet är att alla funktioner \( \; y \, = \, f(x) \; \) vi behandlar är kontinuerliga i alla punkter av det betraktade området.
Regler om växande och avtagande
 |
Det är derivatans tecken som avgör om
en funktion är växande eller avtagande:
Funktionen \( \; y \, = \, f(x) \; \) är växande för \( \; x = a \; \) om derivatan \( \; f\,'(a) \, {\bf {\color{Red} >}} \, 0 \;. \) Funktionen \( \; y \, = \, f(x) \; \) är avtagande för \( \; x = a \; \) om derivatan \( \; f\,'(a) \, {\bf {\color{Red} <}} \, 0 \;. \) |
Med tecken menas \( \,+\, \) eller \( \,-\, \) som står framför ett tal för att visa om talet är positivt eller negativt.
| Reglerna säger i ord:
Det omvända är också sant:
|
\( \qquad \) | En funktion växer där derivatan är positiv.
En funktion avtar där derivatan är negativ. Derivatan är positiv där funktionen växer. Derivatan är negativ där funktionen avtar. |
Om derivatan \( \, f\,'(a) \; {\bf {\color{Red} =}} \; 0 \, \) är funktionen varken växande eller avtagande för \( \, x = a \, \). Vilka slutsatser man kan dra då, behandlas i nästa avsnitt.
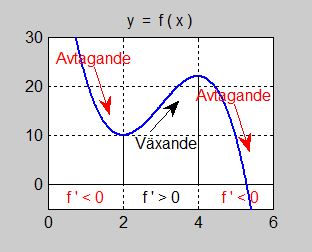
I exempel 1 visas grafen till en funktion som först avtar (negativ derivata), för att sedan växa (positiv derivata). Men hur avgörs detta utan graf (algebraiskt) och framför allt hur beräknas och anges för vilka \( \, x \, \) exakt funktionen är avtagande resp. växande? Detta behandlas i exemplen 1-3 som följer.
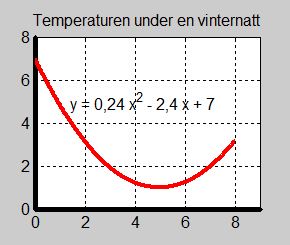
Exempel 1 Vinternatt
 |
Under en vinternatt varierar temperaturen enligt funktionen
där \( y \;\, = \) temperaturen i grader Celsius och \( x \;\, = \) tiden i timmar efter midnatt Funktionen \(\, f(x)\):s definitionsmängd: \( \quad 0 \leq x \leq 8 \) a) Avgör algebraiskt om temperaturen är växande eller avtagande vid:
|
Lösning:
a) För att kunna använda reglerna ovan ställer vi upp derivatan:
- \[ f(x) \, = \, 0,24\,x^2 - 2,4\,x + 7 \]
- \[ f'(x) \, = \, 0,48\,x - 2,4 \]
För att bestämma derivatans tecken måste vi beräkna derivatans värden för de efterfrågade tiderna:
- \( f'(2) \, = \, 0,48 \cdot 2 - 2,4 = -1,44 < 0 \; \Rightarrow \; \) Temperaturen är avtagande vid kl 2.
- \( f'(5) \, = \, 0,48 \cdot 5 - 2,4 \qquad\qquad\! = \, 0 \; \Rightarrow \; \) Temperaturen är varken växande eller avtagande vid kl 5.
- \( f'(7) \, = \, 0,48 \cdot 7 - 2,4 = \;\;\, 0,96 > 0 \; \Rightarrow \; \) Temperaturen är växande vid kl 7.
b)
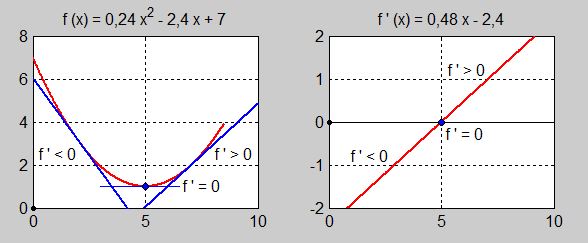
Bilden till vänster visar kurvan \( \, f(x) = 0,24\,x^2 - 2,4\,x + 7 \, \) samt tangenterna till kurvan i \( x = 2 \, , \; x = 5 \) och \( x = 7 \).
- I tidsintervallet \( \, 0 \leq x < 5 \, \) avtar \( \, f(x) \, \) därför att \( \, f\,' < 0 \). Ex.: \( \, f\,'(2) = -1,44 \, \) dvs tangenten i \( \, x = 2 \, \) har negativ lutning.
- Kl \( \, 5 \, \) på morgonen har temperaturen \( \, f(x) \, \) nått sitt minimum. Då är \( \, f\,'(5) = 0 \, \) dvs tangenten i \( \, x = 5 \, \) har lutningen \( \, 0 \).
- I tidsintervallet \( \, 5 < x \leq 8 \, \) växer \( \, f(x) \, \) därför att \( \, f\,' > 0 \). Ex.: \( \, f\,'(7) = 0,96 \, \) dvs tangenten i \( \, x = 7 \, \) har positiv lutning.
Bilden till höger visar grafen till derivatan \( \, f\,'(x) = 0,48\,x - 2,4 \, \) som en rät linje.
- I tidsintervallet \( \, 0 \leq x < 5 \, \) är derivatan negativ:\( \, f\,' < 0 \). Räta linjen ligger under \( \, x\)-axeln.
- I punkten \( \, x = 5 \, \) är derivatan \( \, 0 \): Räta linjen skär \( \, x\)-axeln.
- I tidsintervallet \( \, 5 < x \leq 8 \, \) är derivatan positiv: \( \, f\,' > 0 \). Räta linjen ligger över \( \, x\)-axeln.
Att derivatans graf är en rät linje beror på att funktionen \( \, f(x) \, \) är en 2:a gradsfunktion, se Derivatan av en kvadratisk funktion.
Ett kompakt sätt att studera en funktion är att använda en s.k. teckentabell. Att arbeta med en teckentabell kallas teckenstudium, vilket innebär att med hjälp av derivatans tecken dra slutsatser om funktionens växande resp. avtagande. Närmare bestämt bestämmer man derivatans tecken kring derivatans nollställen.
Exempel 2 Teckenstudium
| Följande teckentabell är given:
|
Använd teckentabellen för att ange när funktionen \( \, y = f(x) \, \) är växande och när den är avtagande.
a) Fyll i dina svar på de platser i tabellen där det står ett frågetecken (?). Använd i tabellen symbolen ↗ för växande och symbolen ↘ för avtagande. b) Ange dina svar med hjälp av olikheter eller intervall på \( \,x\)-axeln. c) Skissa en graf till funktionen \(\, y = f(x) \) som endast visar det kvalitativa (ungefärliga) förloppet av kurvan \(\, y = f(x) \). |
Lösning:
a) Där derivatan är negativ är funktionen avtagande. Där derivatan är positiv är funktionen växande. Således:
| \(x\) | \(2\) | \(4\) | |||
| \( f\,'(x) \) | \(-\) | \(0\) | \(+\) | \(0\) | \(-\) |
| \( f(x) \) | ↘ | ↗ | ↘ |
b) För alla \( \qquad x < 2 \; \) är \(\, f(x) \) avtagande.
I intervallet \( \; 2 < x < 4 \; \) är \(\, f(x) \) växande.
För alla \( \qquad x > 4 \; \) är \(\, f(x) \) avtagande.
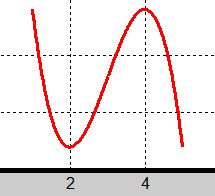
c) Följande graf visar hur grafen till funktionen \(\, y = f(x) \) skulle kunna se ut.
\(\, x\)-värdena är relaterade till kurvan och tabellen, medan \(\, y\)-värdena är obestämda och inte heller relevanta här.
Praktisk anmärkning:
Ställer man själv upp en teckentabell borde man av praktiska skäl se till att \(\,x \)-värdena dvs derivatans nollställen i tabellen är ordnade (sorterade) efter storlek precis som på \(\,x \)-axeln.
Teoretisk anmärkning:
Avgörande för att teckenstudium är en korrekt algebraisk metod är förutsättningen vi gjorde inledningsvis, nämligen att \( \; y \, = \, f(x) \; \) är kontinuerlig i alla punkter av det betraktade området.
Exempel 3 Företagsvinst
Efter statistiska observationer har man kommit fram till att ett företags vinst kan beräknas enligt funktionen:
- \[ V(t) \; = \; -3\,t^3\,+\,27\,t^2\,-\,72\,t\,+\,60 \]
där \( V \; = \) företagets vinst i \( 1\,000 \) kr och
\( t \;\, = \) tiden i antalet år efter årsskiftet 2009/2010 \(. \qquad \) Definitionsmängd: \( \; 1 \leq t \leq 5 \)
I vissa tider ökar vinsten, i andra avtar vinsten.
a) Rita graferna till vinstfunktionen \( V(t) \, \) och dess derivata i separata koordinatsystem.
b) Använd och tolka graferna i a) för att besvara frågan:
För vilka värden på \( t \, \) är funktionen \( V(t) \, \) växande och för vilka värden är den avtagande?
Dvs under vilka tidsperioder ökar vinsten och under vilka minskar vinsten?
c) Bekräfta dina grafiska resultat från b) med några algebraiska beräkningar.
Lösning:
a) Vinstfunktionen samt derivatan:
- \[ V(t) \, = \, -3\,t^3 + 27\,t^2 - 72\,t + 60 \]
- \[ V'(t) \, = \, -9\,t^2 + 54\,t - 72 \]
b) Grafen till vänster visar att Vinstfunktionen \( V(t) \, \)
- avtar för alla \( t \, \) med \( \; 1 \leq t < 2 \)
- växer för alla \( t \, \) med \( \; 2 < t < 4 \)
- avtar för alla \( t \, \) med \( \; 4 < t \leq 5 \)
Grafen till höger visar att derivatan \( V\,'(t) \) till vinstfunktionen är
- negativ (under \( \, t\)-axeln) för alla \( t \, \) med \( \; 1 \leq t < 2 \)
- positiv (över \( \, t\)-axeln) för alla \( t \, \) med \( \; 2 < t < 4 \)
- negativ (under \( \, t\)-axeln) för alla \( t \, \) med \( \; 4 < t \leq 5 \)
Överallt där derivatan är negativ avtar vinstfunktionen. Överallt där derivatan är positiv växer vinstfunktionen.
c) För att bestämma derivatans tecken beräknas derivatans värden för vissa tider ur de tre intervallen från b):
- \( V'(1) \, = \, -9 \cdot 1^2 + 54 \cdot 1 - 72 = -27 < 0 \; \Rightarrow \; \) Vinsten är avtagande för t = 1.
- \( V'(3) \, = \, -9 \cdot 3^2 + 54 \cdot 3 - 72 = {\color{White} {-2}} 9 > 0 \; \Rightarrow \; \) Vinsten är växande för t = 3.
- \( V'(5) \, = \, -9 \cdot 5^2 + 54 \cdot 5 - 72 = -27 < 0 \; \Rightarrow \; \) Vinsten är avtagande för t = 5.
Medelvärdessatsen
Den teoretiska grunden för reglerna om växande och avtagande av funktioner är den s.k. medelvärdessatsen, ibland kallad även differentialkalkylens medelvärdessats.
Vi formulerar satsen här utan bevis för att få en bättre förståelse för regeln ovan, men även för att kunna lösa vissa övningar på A-nivå (övn 9-11).
Medelvärdessatsen:
i intervallet \( \, a < x < b \, \). |
 |
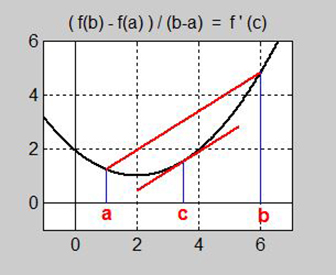Därmed säger medelvärdessatsen att funktionens genomsnittliga förändringshastighet i hela intervallet är lika med derivatan \(-\) den exakta förändringshastigheten \(-\) i någon punkt \( \, c \) inuti intervallet.
Bilden till höger illustrerar medelvärdessatsen: Sekanten till kurvan \( \,y = f(x) \) över intervallet \( \, a < x < b \, \) har samma lutning som tangenten till kurvan i någon punkt \( \, c \, \) inuti intervallet, vilket är den geometriska tolkningen till att den genomsnittliga förändringshastigheten i hela intervallet är lika med derivatan i punkten \( \, c \).
Om man tolkar den genomsnittliga förändringshastigheten som derivatans medelvärde i intervallet, förstår man satsens beteckning. Någonstans i intervallet \(-\) i punkten \( \, c -\) antar derivatan sitt medelvärde. Det sägs ingenting om hur man hittar denna punkt \( \, c \, \). Medelvärdessatsen säger bara att en sådan punkt alltid existerar. Därför kallar man den också för en existenssats. Den högre matematiken är full av sådana existenssatser.
Den för oss praktiskt relevanta slutsatsen ur medelvärdessatsen är att den ger oss reglerna om växande och avtagande. För att visa detta kan man skriva om satsens formel:
- \[\begin{array}{rcl} {f(b) \, - \, f(a) \over b - a} & = & f\,'\,(c) \\ f(b) \, - \, f(a) & = & f'(c) \, \cdot \, (b - a) \end{array}\]
Sedan kan man genom att skilja mellan de två olika fallen \( \,a > b \) och \( \,a < b \), resonera sig fram till reglerna om växande och avtagande av funktionen \( \, f(x) \) i punkten \( \, c \). Vi hoppar över det formella beviset. Istället ska vi i övningarna 9-11 försöka att hitta denna okända punkt vars existens medelvärdessatsen teoretiskt garanterar.
Copyright © 2011-2015 Taifun Alishenas. All Rights Reserved.
