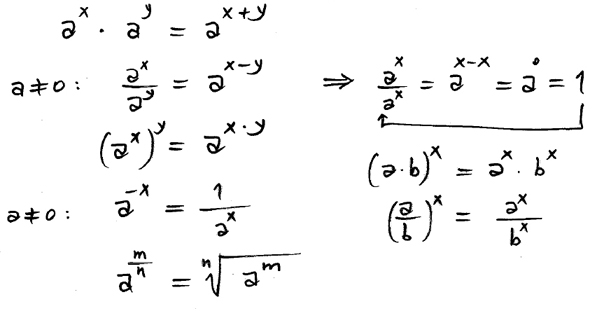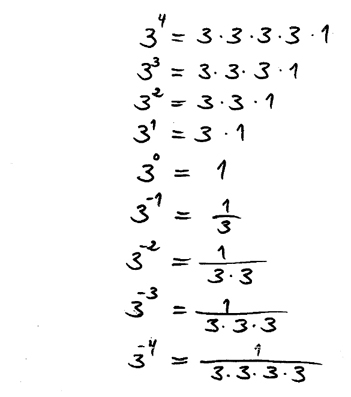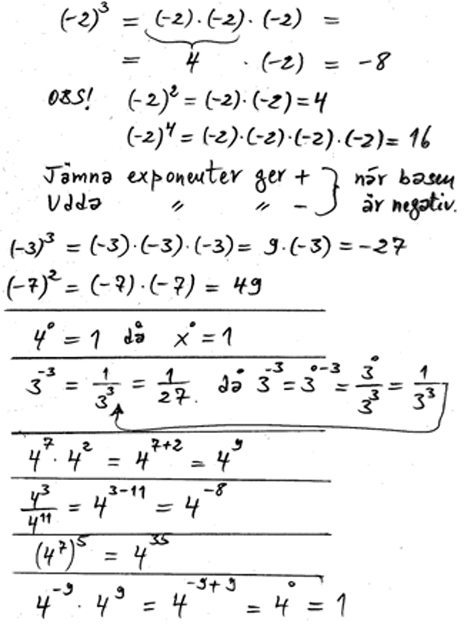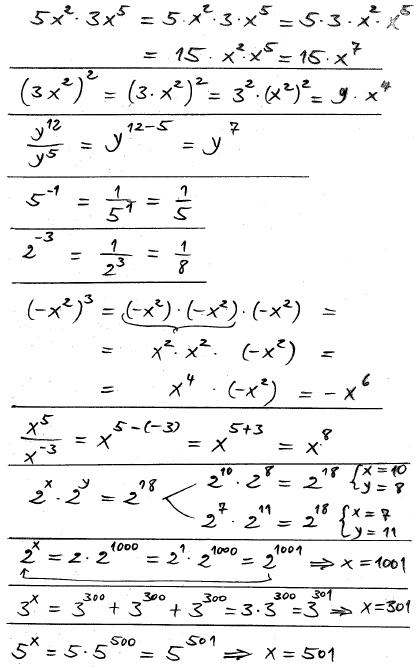1.5 Potenslagarna

Teori

Övningar

Några begrepp

Ett uttryck av formen \( a^x\, \) läses "a upphöjt till x" och kallas potens. \( a\, \) heter basen och \( x\, \) exponenten.

Om \( x\, \) är ett positivt heltal och \( a\, \) ett tal \( \neq 0 \) kan potensen \( a^x\, \) definieras som en förkortning för upprepad multiplikation av \( a\, \) med sig själv:

\[ a^x = \underbrace{a \cdot a \cdot a \cdot \quad \ \cdots \quad \cdot a}_{x} \]

T.ex.:

\[ a^2 = a \cdot a \]

\[ a^3 = a \cdot a \cdot a \]

Att ta \( a\, \) upphöjt till \( x\, \) är en räkneoperation som kallas exponentiering. När \( x=2\, \) pratar man om kvadrering.

Anta att \( x\, \) är en okänd variabel och \( b\, \) och \( c\, \) givna konstanter \( \neq 0 \) . Då kallas

funktioner av typ \( y = 10^x\, \) exponentialfunktioner, generellt\[ y = c \cdot a^x\, \].

ekvationer av typ \( 10^x\,= 125 \) exponentialekvationer, generellt\[ a^x\, = b \].

funktioner av typ \( y = x^3\, \) potensfunktioner, generellt\[ y = x^b\, \].

ekvationer av typ \( x^3\, = 8 \) potensekvationer, generellt\[ x^b\, = c \].

Medan exponentialekvationer löses genom logaritmering (se avsnitt 1.7 Logaritmer), löses potensekvationer genom rotdragning, t.ex:

\[\begin{align} x^3 & = 8 \qquad & | \; \sqrt[3]{\;\;} \\ \sqrt[3]{x^3} & = \sqrt[3]{8} \\ x & = 2 \\ \end{align}\]

Alternativt (med bråk som exponent):

\[\begin{align} x^3 & = 8 \qquad & | \; (\;\;\;)^{1 \over 3} \\ (x^3)^{1 \over 3} & = 8^{1 \over 3} \\ x^{3\cdot{1 \over 3}} & = 8^{1 \over 3} \\ x & = 2 \\ \end{align}\]

Den alternativa lösningsmetoden använder sig av potenslagar som behandlas nedan. De gäller även för exponenter som är negativa eller bråktal, även om vi inledningsvis definierade potensbegreppet för enkelhets skull endast för positiva heltalsexponenter.

Potenslagarna

Följande lagar gäller för potenser, där basen \( a\, \) är ett tal \( \neq 0 \) och exponenterna \( x\, \) och \( x\, \) vilka rationella tal som helst.

Bevis av några potenslagar

Påstående (Produkt av potenser med samma bas):

\[ a^x \cdot a^y \; = \; a^{x+y} \]

Bevis:

Påståendet kan bevisas genom att använda potensens definition:

\[ a^x \cdot a^y \; = \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{x} \; \cdot \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{y} \; = \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{x+y} \; = \; a^{x+y} \]

Påstående (Nollte potens):

\[ a^0 \; = \; 1 \]

Bevis:

Påståendet kan bevisas genom att använda potenslagen för division av potenser med samma bas:

\[ a^0 \; = \; a^{x-x} \; = \; {a^x \over a^x} \; = \; 1 \]

Påstående (Negativ exponent):

\[ a^{-x} \; = \; {1 \over a^x} \]

Bevis:

Påståendet kan bevisas genom att använda potenslagen för division av potenser med samma bas samt lagen om nollte potensen:

\[ a^{-x} \; = \; a^{0-x} \; = \; {a^0 \over a^x} \; = \; {1 \over a^x} \]

Exempel på potenslagars användning

---

---