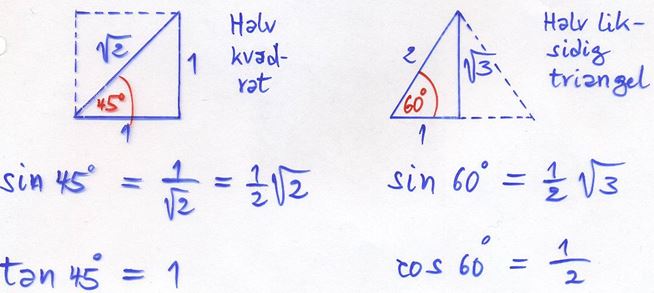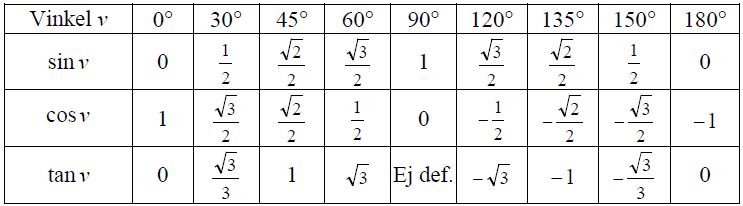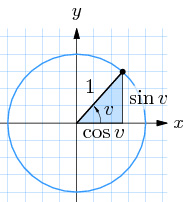Kapitel 5 Trigonometri

<-- Förra kapitel

Start Matte 3c

Planering Matte 3c

Formelsamling Trigonometri

Utdrag ur planeringen:

Fil:Planering Trigonometria.jpg

5.1 Trigonometri i rätvinkliga trianglar

Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 208

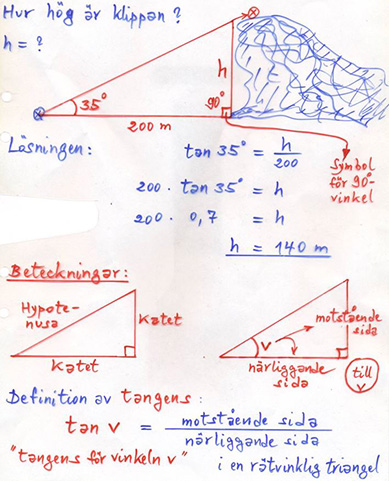
Tangens för \( \, v \, < \, 90^\circ \)

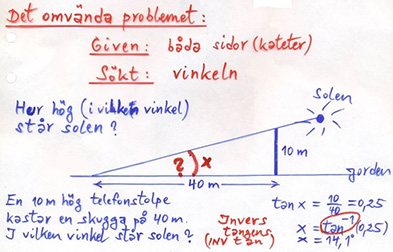
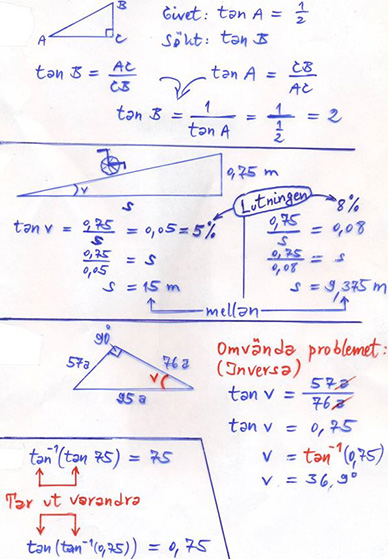
Exempel på tangens

Sinus och Cosinus för \( \, v \, < \, 90^\circ \)

5.2 Exakta trigonometriska värden / Enhetscirkeln

Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 209 / 210

Två speciella vinklar: \( \, 45^\circ \, \) och \( \, 60^\circ \, \)

Pythagoras satsen används på halva kvadraten med sidan \( \, 1 \, \) för att få diagonalen \( \, \sqrt{2} \). Sedan bestäms \( \, \sin 45^\circ \, \) och \( \, \tan 45^\circ \):

På liknande sätt används Pythagoras på halva liksidiga triangeln med sidan \( \, 2 \, \) för att få höjden \( \, \sqrt{3} \). Sedan bestäms \( \, \sin 60^\circ \) och \( \, \cos 60^\circ \).

"Exakt" betyder: Gå inte över till decimaltal, dvs:

Bibehåll bråk med endast heltal i täljare och nämnare,
Bibehåll rötter som inte ger heltal.

En konsekvens blir att inte ens rötter ska stå kvar i bråkens nämnare. Ta upp dem genom förlängning med \( \, \sqrt{{\color{White} {\cdots}}} \), t.ex.:

\[ \displaystyle \frac{1}{\sqrt{2}} \, = \, \frac{1 \, \cdot \, {\color{Red} {\sqrt{2}}}}{\sqrt{2} \cdot {\color{Red} {\sqrt{2}}}} \, = \, \frac{\sqrt{2}}{2} \, = \, \frac{1}{2} \, \sqrt{2} \]

Ytterligare exakta trigonometriska värden

Andra geometriska satser ger följande exakta värden:

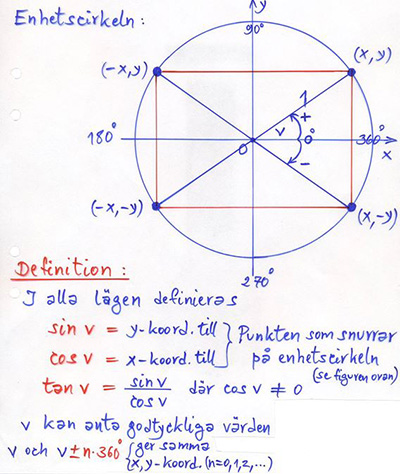
Enhetscirkeln

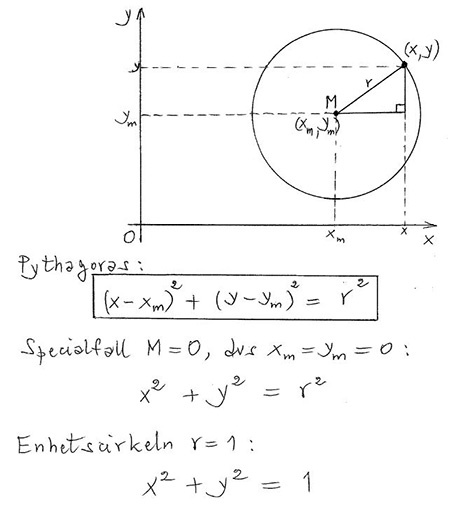
Cirkel \( \, = \, \) Mängden av alla punkter som har samma avstånd (radien \( \, r \, \)) från en punkt (medelpunkten \( \, M \, \)).

Cirkelns ekvation:

Enhetscirkeln är cirkeln med radien \( \, r \, = \, 1 \, \) och medelpunkten \( \, M \, = \, O \, \) (origo).

Om en punkt \( \, P\,(x, y) \, \) snurrar på enhetscirkeln och \( \, v \, \) är vinkeln mellan \( \, x\)-axeln och \( \, \overline{OP} \), så gäller:

\( \qquad\qquad\quad \)

\(\begin{array}{rcl} x & = & \cos v \\ y & = & \sin v \end{array}\)

I cirklar med radien \( \, r \, > \, 1 \, \) förblir vinkeln \( \, v \, \) den samma och därmed \( \, \cos v = \displaystyle \frac{r \cdot \; x}{r} = x \, \) och \( \, \sin v = \displaystyle \frac{r \cdot \; y}{r} = y \), precis som ovan.

Detta används för att definiera de trigonometriska funktionerna i godtyckliga trianglar, dvs för vinklar \( \, v \, \geq \, 90^\circ \, \).

5.3 Godtyckliga trianglar

Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 215

Sinus och Cosinus för vinklar: \( \quad 90^\circ \, \leq \, v \, \leq \, 180^\circ \)

Exempel:

\[ \sin 150^\circ \, = \, \sin (180^\circ - 30^\circ) \, = \, \sin 30^\circ \, = \, \frac{1}{2} \]

\[ \cos 120^\circ \, = \, \cos (180^\circ - 60^\circ) \, = \, -\cos 60^\circ \, = \, -\frac{1}{2} \]

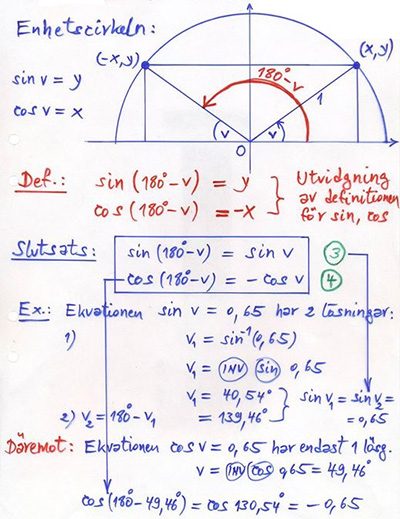
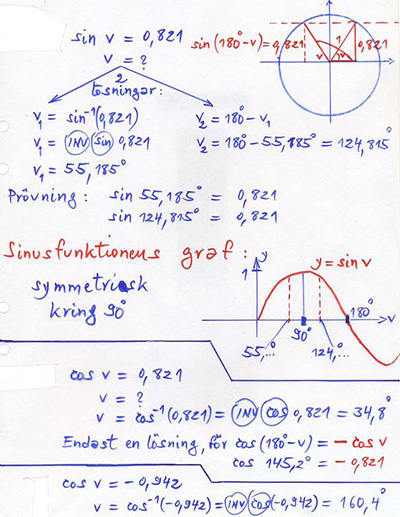
Förklaring med enhetscirkeln:

Punkten till vinkeln \( \, v \, \) har samma \( \, y\)-koordinat (\(=\sin v\)) som punkten till vinkeln \( \, 180-v \).

Punkten till vinkeln \( \, v \, \) har samma \( \, x\)-koordinat (\(=\cos v\)) som punkten till vinkeln \( \, 180-v \, \) med omvänt tecken.

Ekvationer
med

Sin & Cos:

Sinus, Cosinus och Tangens för alla vinklar

5.4 Triangelsatserna: Areasatsen, Sinussatsen, Cosinussatsen

Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 218

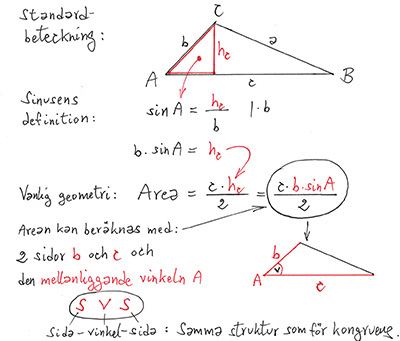
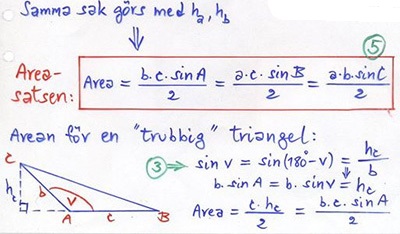
Areasatsen

Formulering utan beteckningar:

En triangels area kan beräknas med areasatsen när två sidor av triangeln och den mellanliggande vinkeln är givna.

Areasatsen med beteckningarna ovan gäller endast för de standardbeteckningar som införts inledningsvis.

Samma gäller för alla formler som följer: Sinussatsen och Cosinussatsen.

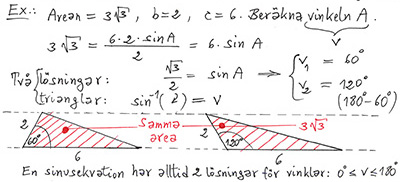
Det omvända problemet:

När arean och två sidor av en triangel är givna och den mellanliggande vinkeln är sökt, ger areasatsen två lösningar och därmed två trianglar:

5.5 Sinussatsen

Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 220 / 224-225

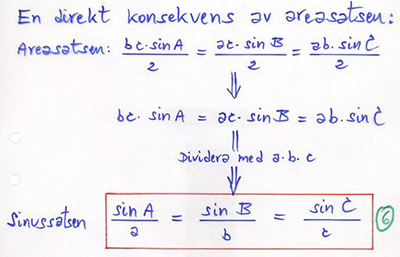
Sinussatsen

Formulering utan beteckningar:

I en triangel är kvoten mellan vinklarnas Sinus och deras motstående sidor lika stor.

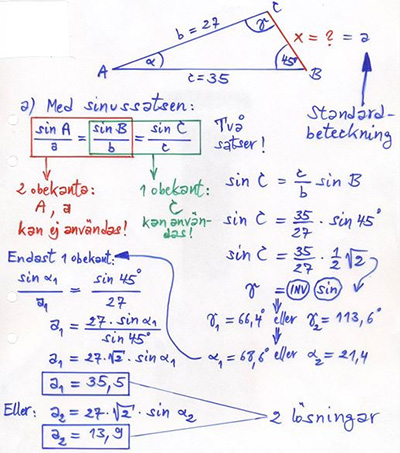
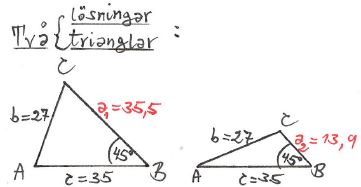
Exempel på sinussatsen (två lösningar)

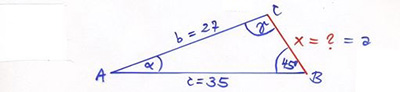
Att det finns två lösningar (två trianglar) beror på att problemet inte har SVS-struktur, dvs:

Triangelns två sidor \( \, b = 27 \, \) och \( \, c = 35 \, \) är givna, men inte den mellanliggande vinkeln, utan den som ligger mittemot \( \, b \).

5.6 Cosinussatsen

Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 229-230

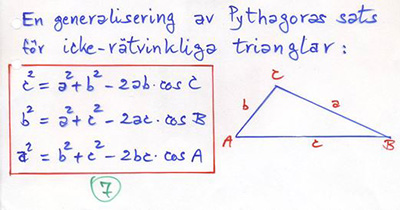
Cosinussatsen

Pythagoras är ett specialfall av cosinussatsen för fallet: \( \quad A , B , {\rm eller\;} C \, = \, 90^\circ \quad \Rightarrow \quad \cos 90^\circ \, = \, 0 \).

Cosinussatsen utvidgar Pythagoras med en term som involverar två sidor och den mellanliggande vinkeln.

När två sidor i en triangel och den mellanliggande vinkeln är givna (SVS-struktur), kan man med cosinussatsen beräkna den tredje sidan (endast en lösning).

När två sidor är givna samt en vinkel som inte ligger mellan dem (icke-SVS-struktur) ger cosinussatsen en andragradsekvation med (i regel) två lösningar, se exemplet nedan.

Samma exempel med cosinussatsen

Att även cosinussatsen ger två lösningar (samma som sinussatsen) bekräftar att det är icke-SVS-strukturen som är orsaken till de två lösningarna.

5.7 Användning av trigonometri

Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 232-233