3.1 Växande och avtagande
| Genomgång | Övningar | Nästa avsnitt >> |
Detta kapitel handlar om att använda derivatan som ett verktyg för att få information om själva funktionen.
Negativ och positiv lutning hos räta linjer
Nu går vi vidare från räta linjer till allmänna funktioner (kurvor).
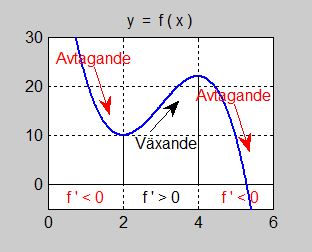
Regler om växande och avtagande för funktioner
I detta första avsnitt används derivatan för att få reda på om funktionen växer eller avtar. För just detta ändamål räcker det till att titta på derivatans tecken.
 |
Det är derivatans tecken (\( \,+\, \) eller \( \,-\, \)) som avgör om en funktion är växande
eller avtagande: Funktionen \( \; y \, = \, f(x) \; \) är växande för \( \; x = a \; \) om derivatan \( \; f\,'(a) \, {\bf {\color{Red} >}} \, 0 \;. \) Funktionen \( \; y \, = \, f(x) \; \) är avtagande för \( \; x = a \; \) om derivatan \( \; f\,'(a) \, {\bf {\color{Red} <}} \, 0 \;. \)
|
Om derivatan \( \, f\,'(a) \; {\bf {\color{Red} =}} \; 0 \, \) är funktionen varken växande eller avtagande för \( \, x = a \, \). Vilka slutsatser man kan dra då, behandlas i nästa avsnitt.
I exemplen 1-3 behandlas hur man algebraiskt avgör om en funktion är växande eller avtagande och hur man beräknar för vilka \( \, x \, \) en funktion är växande resp. avtagande.
Exempel 1 Vinternatt
 |
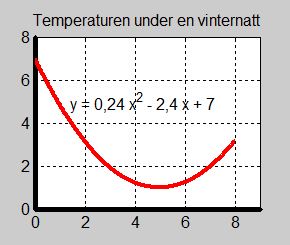Under en vinternatt varierar temperaturen enligt funktionen
där \( y \;\, = \) temperaturen i grader Celsius och \( x \;\, = \) tiden i timmar efter midnatt Funktionen \(\, f(x)\):s definitionsmängd: \( \quad 0 \leq x \leq 8 \) a) Avgör algebraiskt om temperaturen är växande eller avtagande vid:
|
Påminnelse: En funktions definitionsmängd är mängden av alla \( \, x \, \) för vilka funktionen är definierad.
Lösning:
a) För att kunna använda reglerna ovan ställer vi upp derivatan:
- \[ f(x) \, = \, 0,24\,x^2 - 2,4\,x + 7 \]
- \[ f'(x) \, = \, 0,48\,x - 2,4 \]
För att bestämma derivatans tecken måste vi beräkna derivatans värden för de efterfrågade tiderna:
- \( f'(2) \, = \, 0,48 \cdot 2 - 2,4 = -1,44 < 0 \; \Rightarrow \; \) Temperaturen är avtagande vid kl 2.
- \( f'(5) \, = \, 0,48 \cdot 5 - 2,4 \qquad\qquad\! = \, 0 \; \Rightarrow \; \) Temperaturen är varken växande eller avtagande vid kl 5.
- \( f'(7) \, = \, 0,48 \cdot 7 - 2,4 = \;\;\, 0,96 > 0 \; \Rightarrow \; \) Temperaturen är växande vid kl 7.
b)
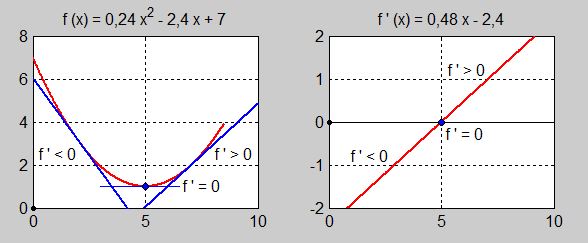
Bilden till vänster visar kurvan \( \, f(x) = 0,24\,x^2 - 2,4\,x + 7 \, \) samt tangenterna till kurvan i \( x = 2 \, , \; x = 5 \) och \( x = 7 \).
- I tidsintervallet \( \, 0 \leq x < 5 \, \) avtar \( \, f(x) \, \) därför att \( \, f\,' < 0 \). Ex.: \( \, f\,'(2) = -1,44 \, \) dvs tangenten i \( \, x = 2 \, \) har negativ lutning.
- Kl \( \, 5 \, \) på morgonen har temperaturen \( \, f(x) \, \) nått sitt minimum. Då är \( \, f\,'(5) = 0 \, \) dvs tangenten i \( \, x = 5 \, \) har lutningen \( \, 0 \).
- I tidsintervallet \( \, 5 < x \leq 8 \, \) växer \( \, f(x) \, \) därför att \( \, f\,' > 0 \). Ex.: \( \, f\,'(7) = 0,96 \, \) dvs tangenten i \( \, x = 7 \, \) har positiv lutning.
Bilden till höger visar grafen till derivatan \( \, f\,'(x) = 0,48\,x - 2,4 \, \) som en rät linje.
- I tidsintervallet \( \, 0 \leq x < 5 \, \) är derivatan negativ:\( \, f\,' < 0 \). Räta linjen ligger under \( \, x\)-axeln.
- I punkten \( \, x = 5 \, \) är derivatan \( \, 0 \): Räta linjen skär \( \, x\)-axeln.
- I tidsintervallet \( \, 5 < x \leq 8 \, \) är derivatan positiv: \( \, f\,' > 0 \). Räta linjen ligger över \( \, x\)-axeln.
Att derivatan är linjär beror på att själva funktionen \( \, f(x) \, \) är en 2:a gradsfunktion, se Derivatan av en kvadratisk funktion.
I fortsättningen och även i hela detta kapitel förutsätts att alla funktioner \( \; y \, = \, f(x) \; \) vi behandlar är kontinuerliga i alla punkter av det betraktade området.
Vad är en teckenstudie ?
Teckenstudie är en metod för att med hjälp av en s.k. teckentabell bestämma var en funktion är växande och var den är avtagande.
Detta gör man genom att kartlägga derivatans nollställen och från derivatans tecken kring nollställena dra slutsatser om växande resp. avtagande.
Exempel 2 Teckenstudie
| Av en funktion är endast en s.k. teckentabell given:
|
a) Fyll i symboler på de platser i tabellen där det står ett frågetecken (?). Använd symbolen ↗ för växande och symbolen ↘ för avtagande. b) Ange dina svar algebraiskt med hjälp av olikheter eller intervall på \( \,x\)-axeln. c) Skissa en graf till funktionen \(\, y = f(x) \) som endast visar det kvalitativa (ungefärliga) förloppet av kurvan \(\, y = f(x) \). |
Lösning:
| a) Där \(f\,'\) har tecknet \(-\) är \(f\) avtagande, där \(f\,'\) har tecknet \(+\) är \(f\) växande:
|
\(\qquad\) | b) För alla \( \; x < 2 \; \) är \(\, f(x) \) avtagande.
|
c)
 |
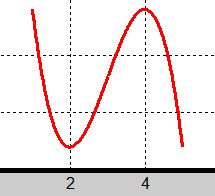I denna skiss är \(\, x\)-värdena relaterade till kurvan och tabellen,
medan \(\, y\)-värdena är obestämda och inte heller relevanta här.
Anmärkning: Avgörande för att teckenstudie är en korrekt algebraisk metod är förutsättningen vi gjorde inledningsvis, nämligen att \( \; y \, = \, f(x) \; \) är kontinuerlig i alla punkter av det betraktade området. |
Exempel 3 Företagsvinst
Efter statistiska observationer har man kommit fram till att ett företags vinst kan beräknas enligt funktionen:
- \[ V(t) \; = \; -3\,t^3\,+\,27\,t^2\,-\,72\,t\,+\,60 \]
där \( V \; = \) företagets vinst i \( 1\,000 \) kr och
\( t \;\, = \) tiden i antalet år efter årsskiftet 2009/2010 \(. \qquad \) Definitionsmängd: \( \; 1 \leq t \leq 5 \)
I vissa tider ökar vinsten, i andra avtar vinsten.
a) Rita graferna till vinstfunktionen \( V(t) \, \) och dess derivata i separata koordinatsystem.
b) Använd och tolka graferna i a) för att besvara frågan:
För vilka värden på \( t \, \) är funktionen \( V(t) \, \) växande och för vilka värden är den avtagande?
Dvs under vilka tidsperioder ökar vinsten och under vilka minskar vinsten?
c) Bekräfta algebraiskt dina grafiska resultat från b).
d) Skriv dina resultat till en teckentabell.
Lösning:
a) Vinstfunktionen samt derivatan:
- \[ V(t) \, = \, -3\,t^3 + 27\,t^2 - 72\,t + 60 \]
- \[ V'(t) \, = \, -9\,t^2 + 54\,t - 72 \]
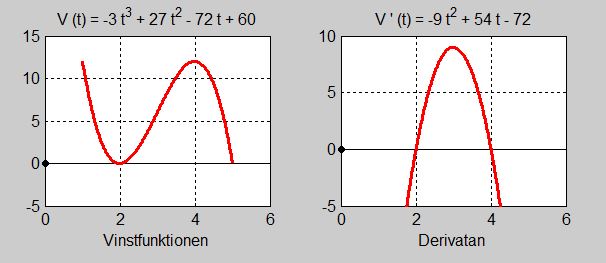
b) Grafen till vänster visar att Vinstfunktionen \( V(t) \, \)
- avtar för alla \( t \, \) med \( \; 1 \leq t < 2 \)
- växer för alla \( t \, \) med \( \; 2 < t < 4 \)
- avtar för alla \( t \, \) med \( \; 4 < t \leq 5 \)
Grafen till höger visar att derivatan \( V\,'(t) \) till vinstfunktionen är
- negativ (under \( \, t\)-axeln) för alla \( t \, \) med \( \; 1 \leq t < 2 \)
- positiv (över \( \, t\)-axeln) för alla \( t \, \) med \( \; 2 < t < 4 \)
- negativ (under \( \, t\)-axeln) för alla \( t \, \) med \( \; 4 < t \leq 5 \)
Överallt där derivatan är negativ avtar vinstfunktionen.
Överallt där derivatan är positiv växer vinstfunktionen.
c) Vi väljer vissa (representativa) tider ur de tre delintervallen från b), t.ex. \( \, {\color{Red} 1} \), \( \, {\color{Red} 3} \) och \( \, {\color{Red} 5} \), för att
- algebraiskt bestämma derivatans tecken:
- \( V'({\color{Red} 1}) \, = \, -9 \cdot 1^2 + 54 \cdot 1 - 72 = -27 < 0 \; \Rightarrow \; \) Vinsten är avtagande för t = 1.
- \( V'({\color{Red} 3}) \, = \, -9 \cdot 3^2 + 54 \cdot 3 - 72 = \quad\; 9 > 0 \; \Rightarrow \; \) Vinsten är växande för t = 3.
- \( V'({\color{Red} 5}) \, = \, -9 \cdot 5^2 + 54 \cdot 5 - 72 = -27 < 0 \; \Rightarrow \; \) Vinsten är avtagande för t = 5.
d) Vi överför resultaten till en teckentabell:
| \(t\) | \({\color{Red} 1}\) | \(2\) | \({\color{Red} 3}\) | \(4\) | \({\color{Red} 5}\) |
| \( V\,'(t) \) | \(-\) | \(0\) | \(+\) | \(0\) | \(-\) |
| \( V(t) \) | ↘ | ↗ | ↘ |
- Pga \( \, V(t)\):s kontinuitet som polynom ger denna teckenstudie en fullständig bild av funktionens
- kvalitativa förlopp som överensstämmer med \( \, V(t)\):s graf i a).
Medelvärdessatsen
De inledningsvis nämnda reglerna om växande och avtagande har sin teoretiska grund i differentialkalkylens medelvärdessats, kort kallad medelvärdessatsen.
Vi formulerar och förklarar här satsen utan bevis för att få en bättre förståelse för reglerna.
|
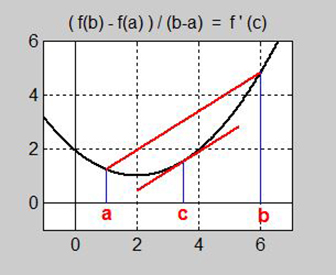
Differentialkalkylens medelvärdessats:
|
Medelvärdessatsen säger att funktionens genomsnittliga förändringshastighet i hela intervallet är lika med derivatan i någon punkt \( \, c \, \) inuti intervallet.
Bilden visar att sekanten till kurvan \( \,y = f(x) \) över intervallet \( \, a < x < b \, \) har samma lutning som tangenten till kurvan i någon punkt \( \, c \, \) inuti intervallet. Det betyder algebraiskt att den genomsnittliga förändringshastigheten i hela intervallet är lika med derivatan i punkten \( \, c \).
Satsens beteckning tolkar den genomsnittliga förändringshastigheten som derivatans medelvärde i intervallet. Någonstans inuti intervallet \(-\) i punkten \( \, c -\) antar derivatan sitt medelvärde.
För att se att medelvärdessatsen ger oss reglerna om växande och avtagande kan man skriva om satsens formel:
- \[\begin{array}{rcl} \displaystyle {f(b) \, - \, f(a) \over b - a} & = & f\,'\,(c) \\ \\ f(b) \, - \, f(a) & = & f'(c) \, \cdot \, (b - a) \end{array}\]
Sedan kan man genom att skilja mellan de två olika fallen \( \,a > b \, \) och \( \,a < b \), resonera sig fram till reglerna. Vi hoppar över det formella beviset.
Istället ska vi sedan i övningarna 9-11 försöka att praktiskt beräkna \( \, c \, \) vars existens medelvärdessatsen teoretiskt garanterar.
Copyright © 2011-2018 Taifun Alishenas. All Rights Reserved.
