2. Introduction to force and gravity
| Theory | Exercises | Video |
Key Points
Newton's First Law
A particle will move with a constant velocity or remain at rest if the resultant force on the particle is zero.
Equilibrium
If the resultant force on a particle is zero, then the forces acting on the particle are said to be in equilibrium.
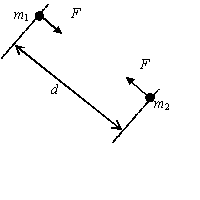
The Universal Law of Gravitation
| \(F=\frac{Gm_{1}m_{2}}{{d}^{\ 2}}\)
\(G=6\textrm{.}67\times 10^{-11}\text{ kg}^{\text{-1}}\text{m}^{\text{3}}\text{s}^{\text{-2}}\) |
|
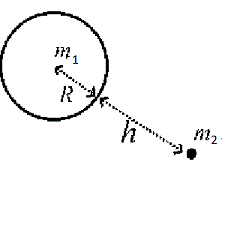
Gravitational force from an heavenly body
| For a particle in the neighbourhood of a planet, moon or star the distance \(d\) is measured from the centre to the particle.
Thus \(d=R+h\), where \(h\) is distance to the surface. |
|
Gravity on Earth
The force of gravity is often called the weight.
\(\begin{align} & F=mg \\ & g=9\textrm{.}8\text{ ms}^{\text{-2}} \\ \end{align}\)
Data
Radius of Earth is \(\text{6}\textrm{.}\text{37}\times \text{1}0^{\text{6}}\text{ }\) metres
Mass of Earth is \(\text{5}\textrm{.}\text{98}\times \text{1}0^{\text{24}}\text{ }\) kg
Describe whether or not the forces acting on the following objects are in equilibrium:
a) A passenger in a train that travels at a constant speed.
b) A hot air balloon rising at a constant rate.
c) A stone dropped into a very deep well full of water.
Solution
a) Yes, if it is travelling in a straight line.
b) Yes, if it is travelling in a straight line.
c) Yes, if it reaches a terminal velocity, so that it is travelling in a straight line at a constant speed.
Find the magnitude of the force of gravity (weight) acting on a lorry of mass 22 tonnes.
Solution
This is calculated using the fact that the weight is given by \(mg\).
\(\begin{align} & mg=22000\times 9\textrm{.}8 \\ & =215600\text{ N} \end{align}\)
The diagram shows the lorry and its weight.
Note that reaction forces also act upwards on each wheel.
\({{R}_{1}}+{{R}_{2}}+{{R}_{3}}+{{R}_{4}}=215600\ \text{N}\)
A box of mass 30 kg is at rest on a table.
a) Calculate the weight of the box.
b) State the magnitude of the upward force that the table exerts on the box.
Solution
a)
\(\begin{align} & W=30\times 9\textrm{.}8 \\ & =294\text{ N} \end{align}\)
b) An upward force of 294 N must act for the box to remain in equilibrium.
A satellite, of mass 400 kg, is at a height of 12 km above the surface of the earth. Find the magnitude of the gravitational attraction on the satellite.
Data\[G=6\textrm{.}67\times {{10}^{-11}}\] \(\text{k}{{\text{g}}^{-\text{1}}}{{\text{m}}^{\text{3}}}{{\text{s}}^{-\text{2}}}\)
Radius of earth \(=6\textrm{.}37\times {{10}^{6}} \text{m} \)
Mass of earth \(=5\textrm{.}98\times {{10}^{24}} \text{kg}\)
Solution
\(\begin{align} & \frac{G{{m}_{1}}{{m}_{2}}}{{{d}^{\ {2}}}}=\frac{6\textrm{.}67\times {{10}^{-11}}\times 400\times 5\textrm{.}98\times {{10}^{24}}}{{{\left( 6\textrm{.}37\times {{10}^{6}}+12000 \right)}^{2}}} \\ & =3917\text{ N} \end{align}\)
The sun has mass \(1\textrm{.}99\times {{10}^{30}} \text{kg}\) . The mean distance of the earth from the sun is approximately \(1\textrm{.}5\times {{10}^{11}} \text{m}\) .
(a) Calculate the force that the sun exerts on the earth.
(b) State the force that the earth exerts on the sun.
(c) Explain why this force varies.
Solution
(a)
\(\begin{align} & \frac{G{{m}_{1}}{{m}_{2}}}{{{d}^{\ 2}}}=\frac{6\textrm{.}67\times {{10}^{-11}}\times 1\textrm{.}99\times {{10}^{30}}\times 5\textrm{.}98\times {{10}^{24}}}{{{\left( 1\textrm{.}5\times {{10}^{11}} \right)}^{2}}} \\ & =3\textrm{.}53\times {{10}^{22}}\text{ N} \end{align}\)
(b) \(3\textrm{.}53\times {{10}^{22}}\text{ N} \)
(c) The distance between the earth and the sun varies.