Skillnad mellan versioner av "2.6 Derivatan av exponentialfunktioner"

Derivatan av exponentialfunktionen \( \, y = e\,^x \) med \( \,e = \) Eulers tal

Påstående

Frågeställningen ovan har i matematikens historia motiverat den schweiziske matematikern Leonard Euler att ställa upp sin berömda formel för beräkning av talet \( \, e \, \) som vi redan använde i Hur kom(mer) talet \( \, e \,\) till? och som vi nu \(-\) efter att ha behandlat limesbegreppet \(-\) kan formulera så här:

\[ \lim_{n \to \infty} {\left(1 + {1 \over n}\right)^n} \; =\; e \; = \; 2,718281828\ldots \]

På 1700-talet bevisade Euler denna formel, varför talet \( \, e \, \) kallats efter honom. Vi följer här Eulers bevis som kommer att visa att den efterfrågade basen i frågeställningen ovan är just talet \( \, e \).

Eulers bevis

Vi antar att det finns en bas \( \,b \, > \, 0 \) \(-\) som än så länge är okänd \(-\) så att:

\[\begin{array}{lclcl} y & = & f\,(x) & = & b\,^x \\ {\color{Red} {y\,'}} & {\color{Red} =} & {\color{Red} {f\,'\,(x)}} & {\color{Red} =} & {\color{Red} {b\,^x}} \end{array}\]

I den andra raden har vi formulerat kravet: derivatan = funktionen.

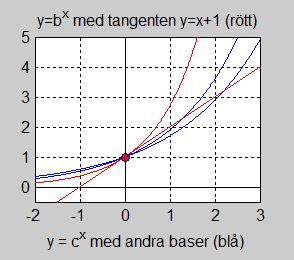
Nu konstruerar vi tangenten till \( y = b\,^x \) i punkten \( \,x = 0 \):

Ekvationen för tangenten till kurvan \( y = b\,^x \) i punkten \( \,x = 0 \) har \(\,k\)-formen    \( y \, = \, k\,x \, + \, m \, \) .

För att bestämma \( \, k \) konstaterar vi att tangenten till kurvan    \( y = b\,^x \)    i    \( \,x = 0 \)    har samma lutning \(\,k\) som funktionens derivata i denna punkt.

Pga kravet \( \, {\color{Red} {f\,'(x) = b\,^x}} \, \) (se ovan) blir det: \[ k \, = \, {\color{Red} {f\,'(0) \, = \, b\,^0}}\, = \, 1 \] Tangentens ekvation blir \( \, y \, = \, x \, + \, m \, \) i vilken vi sätter in tangeringspunktens koordinater \( \, (0, 1) \, \) för att bestämma \( \, m \, \): \[\begin{array}{rcl} y & = & x \, + \, m \\ 1 & = & 0 \, + \, m \\ 1 & = & m \end{array}\] Således blir tangentens ekvation    \( \boxed{y \, = \, x \, + \, 1} \)

\( \qquad\qquad \)

Andra exponentialfunktioner \( \, y = c\,^x \, \) med \( \, c \neq b \, \) skär denna tangent, medan \( \, y = b\,^x \, \) med \( \, y\,' = b\,^x \, \) tangerar den.

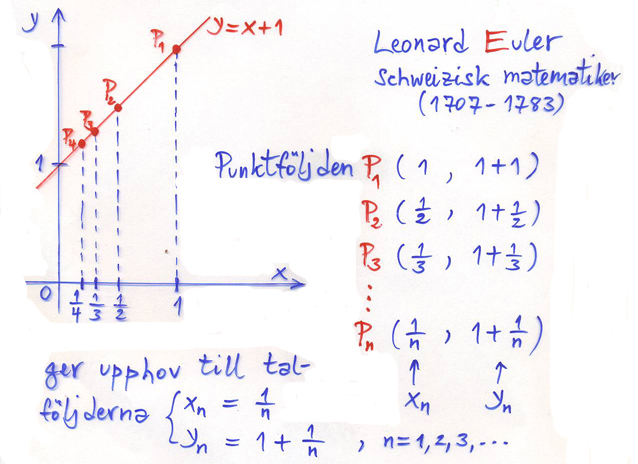
På tangenten \( \, y = x + 1 \, \) konstruerar vi en punktföljd    \( P_1, \, P_2, \, P_3, \, \ldots \)    vars \( \,x\)-koordinater \( \, x_n \, \) bildar talföljden:

\[ 1, \, {1 \over 2}, \, {1 \over 3}, \, {1 \over 4}, \, \ldots \quad {\rm dvs} \quad x_n \, = \, {1 \over n} \qquad {\rm som\;allmän \;term,\;där:} \qquad n = 1,\,2,\,3,\,\ldots \]

Talföljden \( \,x_n \, \) ger pga \( \, y = x + 1 \, \) upphov till en talföljd \( \,y_n \, = \, x_n + 1 \, = \, {1 \over n} + 1 \, = \, 1 \, + \, {1 \over n} \, \) på \( \,y\)-axeln:

\(y_n = 1 + {1 \over n} : \;\; 1\!+\!1, \quad 1\!+\!{1 \over 2}, \quad 1\!+\!{1 \over 3}, \quad 1\!+\!{1 \over 4}, \, \ldots \) Punkterna \( \, P_n = (x_n, \; y_n) = \left({1 \over n}, \; 1 + {1 \over n}\right) \, \) går mot tangeringspunkten \( \, (0, 1) \, \) när \( \, n \to \infty \). Genom varje punkt \( \, P_n \, \) går en exponentialfunktion \( \, y_n = b_n\,^{x_n} \, \) med en speciell bas \( \, b_n \). Dvs punktföljden \( \, P_n \, \) ger upphov till följden \( \, y_n = b_n\,^{x_n} \), där: \( \qquad\quad b_n \to \, b \quad\; {\rm när} \quad\; n \to \infty \) Vi sätter in punktföljdernas allmänna termer \( \, x_n = {1 \over n} \) och \( \, y_n = 1 + {1 \over n} \, \) i funktionerna \( \, y_n = b_n\,^{x_n}\,\) och får: \[\begin{array}{rcll} y_n & = & b_n\,^{x_n} \\ 1 + {1 \over n} & = & b_n\,^{1 \over n} \qquad & | \quad (\,\cdot\,)\,^n \\ \\ \left(1 + {1 \over n}\right)^n & = & b_n \end{array}\] Detta är Eulers formel som ger oss Eulers tal:

\( \displaystyle \lim_{n \to \infty} {\left(1 + {1 \over n}\right)^n} \, = \, \lim_{n \to \infty} {b_n} \, = \, b \, = \, 2,718281828\ldots \, = \, e \, \), vilket vi numeriskt hade fått fram i Hur kom(mer) talet \( \, e \,\) till?  :

\( n \)	\( 1\,000 \)	\( 1000\,000 \)	\( 1000\,000\,000 \)	\( 10\,000\,000\,000 \)	\( \to \infty \)
\( \left(1 + {1 \over n}\right)^n \)	\( {\color{Red} {2,71}}6923932\ldots \)	\( {\color{Red} {2,71828}}0469\ldots \)	\( {\color{Red} {2,71828182}}7\ldots \)	\( {\color{Red} {2,718281828\ldots}} \)	\( \quad \to \; {\color{Red} {{\rm Eulers\;tal\;} e}} \quad \)

Den inledande frågan i bevisidén:

Kan basen \( \, b \, \) väljas så att derivatan av \( \; y = b\,^x \; \) blir \( \; y\,' = b\,^x \)   ?

kan nu besvaras så här:

Ja, om vi väljer basen \( \, b \, \) som \( \, {\color{Red} e} \, = \, \) Eulers tal blir derivatan av \( \; y = e\,^x \; \) \( \; {\color{Red} {y\,' = e\,^x}}\) .

Deriveringsregeln för \( y = C\,e\,^{k\,x} \)

När konstanter är inblandade i exponentialuttrycket har vi:

\( \, \bf e \, \) är en konstant, ingen variabel.

Derivatan av exponentialfunktionen \( \, y = a\,^x \)

Från att ha ställt upp deriveringsregeln för \( \, y = e\,^x \, \) är det bara ett enkelt steg till den allmänna exponentialfunktionen \( \, y = a\,^x \, \) med en godtycklig bas \( a > 0\, \):

Påstående

Specialfallet \( \, a = e \, \) och \( \ln a = \ln e = 1 \, \) ger derveringsregeln \( \,y\,' = e^x \, \) för exponentialfunktionen med basen \( \, e \).

Bevis

Vi börjar med att skriva om basen \( \, a \, \) till \( \,e\,^{\ln a} \, \), vilket är möjligt pga inversegenskapen. Då blir det:

\[\begin{array}{rcll} y & = & a\,^x \qquad & : \quad a \, = \,e\,^{\ln a} {\rm \;enligt\;inversegenskapen} \\ y & = & \left(e\,^{\ln a}\right)^x \qquad & : \quad {\rm 3:e\;potenslagen\;på\;HL} \\ y & = & e\,^{(\ln a) \, \cdot \, x} \qquad & : \quad \ln a \, = \, k \\ y & = & e\,^{k \, \cdot \, x} \qquad & | \quad {\rm Derivera\;enligt\;regeln\;ovan} \\ y\,' & = & k \, \cdot \, e\,^{k\,x} \qquad & : \quad k \, = \, \ln a \\ y\,' & = & (\ln a) \, \cdot \, e\,^{(\ln a)\,x} \qquad & : \quad {\rm 3:e\;potenslagen\;på\;HL} \\ y\,' & = & (\ln a) \, \cdot \, \left(e\,^{\ln a}\right)^x \qquad & : \quad e\,^{\ln a} \, = a\, {\rm \;enligt\;inversegenskapen} \\ y\,' & = & (\ln a) \, \cdot \, a^x \\ y\,' & = & a^x \, \cdot \, \ln a \end{array}\]

Deriveringsregeln för \( y = C\,a\,^{k\,x} \)

När konstanter är inblandade har vi:

Uppdaterad tabell över deriveringsregler

Vi utvidgar tabellen över deriveringsregler från förra avsnitt med våra nya resultat i detta avsnitt. I följande tabell är \( C,\,c,\,a,\,k,\,m,\,n \) konstanter medan \( x\, \) och \( y\, \) är variabler: