Skillnad mellan versioner av "2.6 Derivatan av exponentialfunktioner"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 163: | Rad 163: | ||
margin-left: 10px !important; | margin-left: 10px !important; | ||
padding:10px 20px 10px 20px; | padding:10px 20px 10px 20px; | ||
| − | border-radius: 15px;"><b>Ja, om vi väljer <span style="color:red">basen</span> <math> \, b \, </math> som <math> \, {\color{Red} e} \, = \, </math> Eulers tal, blir derivatan av <math> \; y = e\,^x \; </math> <math> \; {\color{Red} {y\,' = e\,^x}}</math> .</b> | + | border-radius: 15px;"><b>Ja, om vi väljer <span style="color:red">basen</span> <math> \, b \, </math> som <math> \, {\color{Red} e} \, = \, </math> Eulers tal, då blir derivatan av <math> \; y = e\,^x \; </math> samma som funktionen<span style="color:black">:</span> <math> \; {\color{Red} {y\,' = e\,^x}}</math> .</b> |
</div> | </div> | ||
</small> | </small> | ||
Versionen från 15 november 2016 kl. 11.39
| << Förra avsnitt | Genomgång | Övningar | Nästa avsnitt >> |
Lektion 19 Derivatan av exponentialfunktioner
Målet i detta avsnitt är att ställa upp deriveringsregeln för den allmänna exponentialfunktionen \( \, y = a\,^x \, \) med en godtycklig bas \( a > 0 \). Detta gör vi genom att först härleda derivatan av exponentialfunktionen \( \, y = e\,^x \, \) med basen \( \, e = \) Eulers tal och sedan gå över till godtycklig bas \( \,a \). Därför kan det vara bra att friska upp sina kunskaper om exponentialfunktionen med basen \( e\, \) (Eulers tal) från kapitel 1.
Derivatan av exponentialfunktionen \( \, y = e\,^x \) med \( \,e = \) Eulers tal
Påstående
Derivatan av exponentialfunktionen med basen \( \, e \, \) är funktionen själv:
- \[ \begin{array}{llcl} {\rm Om} & y & = & e\,^x \;\; {\rm där} \;\; e = {\rm Eulers\;tal} \\ {\rm då} & y\,' & = & e\,^x \end{array}\]
Bevisidé
Derivatans definition för \( \, y = f(x) = e\,^x \, \) leder till:
\[ y\,' = \lim_{h \to 0}\,{f(x + h) - f(x) \over h} = \lim_{h \to 0}\,{e\,^{x + h} - e\,^x \over h} = \lim_{h \to 0}\,{e\,^x \cdot e\,^h - e\,^x \over h} = \lim_{h \to 0}\,{e\,^x \, (e\,^h - 1) \over h} = e\,^x \cdot \lim_{h \to 0}\,{e\,^h - 1 \over h} \]
För att beräkna den sista limes kan s.k. potensserieutveckling av \( \, e\,^x \, \) användas \(-\) vilket dock inte ingår i Matte 3-kursen.
Därför väljer vi en annan metod.
Vi vänder på steken:
Istället för att fråga efter derivatan, kräver vi derivatan = funktionen och frågar efter en bas som uppfyller detta krav.
Frågeställningen lyder:
Svaret är: Ja, det är basen \( \, b \, = \, e \, = \, {\rm Eulers\;tal} \, = \, 2,718281828\ldots \) som gör att derivatan = funktionen.
Frågeställningen ovan har i matematikens historia motiverat den schweiziske matematikern Leonard Euler att ställa upp sin berömda formel för beräkning av talet \( \, e \, \) som vi redan använde i Hur kom(mer) talet \( \, e \,\) till? och som vi nu \(-\) efter att ha behandlat limesbegreppet \(-\) kan formulera så här:
- \[ \lim_{n \to \infty} {\left(1 + {1 \over n}\right)^n} \; =\; e \; = \; 2,718281828\ldots \]
På 1700-talet bevisade Euler denna formel, varför talet \( \, e \, \) kallats efter honom. Vi följer här Eulers bevis som kommer att visa att den efterfrågade basen i frågeställningen ovan är just talet \( \, e \).
Eulers bevis
Vi antar att det finns en bas \( \,b \, > \, 0 \) \(-\) som än så länge är okänd \(-\) så att:
- \[\begin{array}{lclcl} y & = & f\,(x) & = & b\,^x \\ {\color{Red} {y\,'}} & {\color{Red} =} & {\color{Red} {f\,'\,(x)}} & {\color{Red} =} & {\color{Red} {b\,^x}} \end{array}\]
I den andra raden har vi formulerat kravet: derivatan = funktionen.
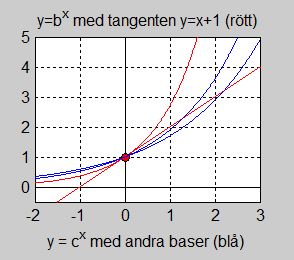
Nu konstruerar vi tangenten till \( y = b\,^x \) i punkten \( \,x = 0 \):
Ekvationen för tangenten till kurvan \( y = b\,^x \) i punkten \( \,x = 0 \) har \(\,k\)-formen \( y \, = \, k\,x \, + \, m \, \) .
För att bestämma \( \, k \) konstaterar vi att tangenten till kurvan \( y = b\,^x \) i \( \,x = 0 \) har samma lutning \(\,k\) som funktionens derivata i denna punkt.
Pga kravet \( \, {\color{Red} {f\,'(x) = b\,^x}} \, \) (se ovan) blir det:
Tangentens ekvation blir \( \, y \, = \, x \, + \, m \, \) i vilken vi sätter in tangeringspunktens koordinater \( \, (0, 1) \, \) för att bestämma \( \, m \, \):
Således blir tangentens ekvation \( \boxed{y \, = \, x \, + \, 1} \) |
\( \qquad\qquad \) |  |
Andra exponentialfunktioner \( \, y = c\,^x \, \) med \( \, c \neq b \, \) skär denna tangent, medan \( \, y = b\,^x \, \) med \( \, y\,' = b\,^x \, \) tangerar den.
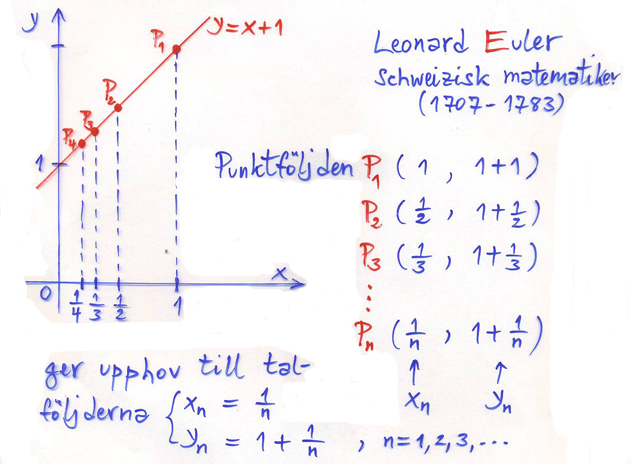
På tangenten \( \, y = x + 1 \, \) konstruerar vi en punktföljd \( P_1, \, P_2, \, P_3, \, \ldots \) vars \( \,x\)-koordinater \( \, x_n \, \) bildar talföljden:
- \[ 1, \, {1 \over 2}, \, {1 \over 3}, \, {1 \over 4}, \, \ldots \quad {\rm dvs} \quad x_n \, = \, {1 \over n} \qquad {\rm som\;allmän \;term,\;där:} \qquad n = 1,\,2,\,3,\,\ldots \]
Talföljden \( \,x_n \, \) ger pga \( \, y = x + 1 \, \) upphov till en talföljd \( \,y_n \, = \, x_n + 1 \, = \, {1 \over n} + 1 \, = \, 1 \, + \, {1 \over n} \, \) på \( \,y\)-axeln:
| \(y_n = 1 + {1 \over n} : \;\; 1\!+\!1, \quad 1\!+\!{1 \over 2}, \quad 1\!+\!{1 \over 3}, \quad 1\!+\!{1 \over 4}, \, \ldots \)
Punkterna \( \, P_n = (x_n, \; y_n) = \left({1 \over n}, \; 1 + {1 \over n}\right) \, \) går mot tangeringspunkten \( \, (0, 1) \, \) när \( \, n \to \infty \). Genom varje punkt \( \, P_n \, \) går en exponentialfunktion \( \, y_n = b_n\,^{x_n} \, \) med en speciell bas \( \, b_n \). Dvs punktföljden \( \, P_n \, \) ger upphov till följden \( \, y_n = b_n\,^{x_n} \), där: \( \qquad\quad b_n \to \, b \quad\; {\rm när} \quad\; n \to \infty \) Vi sätter in punktföljdernas allmänna termer \( \, x_n = {1 \over n} \) och \( \, y_n = 1 + {1 \over n} \, \) i funktionerna \( \, y_n = b_n\,^{x_n}\,\) och får:
Detta är Eulers formel som ger oss Eulers tal: |
 |
\( \displaystyle \lim_{n \to \infty} {\left(1 + {1 \over n}\right)^n} \, = \, \lim_{n \to \infty} {b_n} \, = \, b \, = \, 2,718281828\ldots \, = \, e \, \), vilket vi numeriskt hade fått fram i Hur kom(mer) talet \( \, e \,\) till? :
| \( n \) | \( 1\,000 \) | \( 1000\,000 \) | \( 1000\,000\,000 \) | \( 10\,000\,000\,000 \) | \( \to \infty \) |
| \( \left(1 + {1 \over n}\right)^n \) | \( {\color{Red} {2,71}}6923932\ldots \) | \( {\color{Red} {2,71828}}0469\ldots \) | \( {\color{Red} {2,71828182}}7\ldots \) | \( {\color{Red} {2,718281828\ldots}} \) | \( \quad \to \; {\color{Red} {{\rm Eulers\;tal\;} e}} \quad \) |
|---|
Den inledande frågan i bevisidén:
kan nu besvaras så här:
Deriveringsregeln för \( y = C\,e\,^{k\,x} \)
När konstanter är inblandade i exponentialuttrycket har vi:
Regel: \[ \begin{array}{ll} {\rm Derivatan\;av} & y \;\, = \; C\;e\,^{k\,x} \;\; {\rm där} \;\; C,\,k = {\rm const.} \\ {\rm är} & y\,' = \; C\cdot k\cdot e\,^{k\,x} \end{array}\] Delbevis om \( \, C \, \): Förväxla denna regel inte med Regeln om derivatan av en potens. \( y \, = \, C\,e\,^{k\,x} \, \) är ingen potens- utan en exponentialfunktion, därför att \( \, x \, \) förekommer i exponenten, inte i basen. |
\( \quad \) | Exempel 1 För funktionen \( \;\, f(x) \; = \; 2\,e\,^{-\,x} \; \) blir derivatan:
Exempel 2 För funktionen \( f(x) \; = \; -4\,e\,^{-3\,x} \; \) blir derivatan:
|
OBS! För funktionen \( \, f(x) = e\,^2 \, \) blir derivatan: \( \; f\,'(x) = 0 \; \) därför att \( \, e\,^2 \, \) är en konstant, närmare bestämt \( \, 7,389\ldots \, \).
\( \, e \, \) är en konstant, ingen variabel. Samma sak är det med \( \, a \, \) som vi nu gå över till:
Derivatan av exponentialfunktionen \( \, y = a\,^x \)
Från att ha ställt upp deriveringsregeln för \( \, y = e\,^x \, \) är det bara ett enkelt steg till den allmänna exponentialfunktionen \( \, y = a\,^x \, \) med en godtycklig bas \( a > 0\, \):
Påstående
- \[ \begin{array}{llcl} {\rm Om} & y & = & a\,^x \;\; {\rm där} \;\; a = {\rm godtycklig\;konstant} \, > \,0 \\ {\rm då} & y\,' & = & a\,^x \, \cdot \, \ln a \end{array}\]
Specialfallet \( \, a = e \, \) och \( \ln a = \ln e = 1 \, \) ger derveringsregeln \( \,y\,' = e^x \, \) för exponentialfunktionen med basen \( \, e \).
Bevis
Vi börjar med att skriva om basen \( \, a \, \) till \( \,e\,^{\ln a} \, \), vilket är möjligt pga inversegenskapen. Då blir det:
- \[\begin{array}{rcll} y & = & a\,^x \qquad & : \quad a \, = \,e\,^{\ln a} {\rm \;enligt\;inversegenskapen} \\ y & = & \left(e\,^{\ln a}\right)^x \qquad & : \quad {\rm 3:e\;potenslagen\;på\;HL} \\ y & = & e\,^{(\ln a) \, \cdot \, x} \qquad & : \quad \ln a \, = \, k \\ y & = & e\,^{k \, \cdot \, x} \qquad & | \quad {\rm Derivera\;enligt\;regeln\;ovan} \\ y\,' & = & k \, \cdot \, e\,^{k\,x} \qquad & : \quad k \, = \, \ln a \\ y\,' & = & (\ln a) \, \cdot \, e\,^{(\ln a)\,x} \qquad & : \quad {\rm 3:e\;potenslagen\;på\;HL} \\ y\,' & = & (\ln a) \, \cdot \, \left(e\,^{\ln a}\right)^x \qquad & : \quad e\,^{\ln a} \, = a\, {\rm \;enligt\;inversegenskapen} \\ y\,' & = & (\ln a) \, \cdot \, a^x \\ y\,' & = & a^x \, \cdot \, \ln a \end{array}\]
Deriveringsregeln för \( y = C\,a\,^{k\,x} \)
När konstanter är inblandade har vi:
Derivatan av exponentialfunktionen \( y = C\,a\,^{k\,x} \) med godtycklig bas \( \, a > 0 \) och \( C,\,k = {\rm const.} \)
- \[ \begin{array}{llcl} {\rm Om} & y & = & C\,a\,^{k\,x} \;\; {\rm där} \;\; a > 0,\;\; C,\,k = {\rm const.} \\ {\rm då} & y\,' & = & C\cdot k\cdot a\,^{k\,x} \cdot \ln a \end{array}\]
Uppdaterad tabell över deriveringsregler
Vi utvidgar tabellen över deriveringsregler från förra avsnitt med våra nya resultat i detta avsnitt. I följande tabell är \( C,\,c,\,a,\,k,\,m,\,n \) konstanter medan \( x\, \) och \( y\, \) är variabler:
| \( y\, \) | \( y\,' \) |
|---|---|
| \( c\, \) | \( 0\, \) |
| \( x\, \) | \( 1\, \) |
| \( a\; x \) | \( a\, \) |
| \( k\; x \, + \, m \) | \( k\, \) |
| \( x^2\, \) | \( 2\,x \) |
| \( a\,x^2 \) | \( 2\,a\,x \) |
| \( x^n\, \) | \( n\cdot x\,^{n-1} \) |
| \( a\,x\,^n \) | \( a\cdot n\cdot x\,^{n-1} \) |
| \( \displaystyle {1 \over x} \) | \( \displaystyle - {1 \over x^2} \) |
| \( \sqrt{x} \) | \( \displaystyle {1 \over 2\, \sqrt{x}} \) |
| \( e\,^x \) | \( e\,^x \) |
| \( e\,^{k\,x} \) | \( k\cdot e\,^{k\,x} \) |
| \( C\cdot e\,^{k\,x} \) | \( C\cdot k\cdot e\,^{k\,x} \) |
| \( a\,^x \) | \( a\,^x \cdot \ln a \) |
| \( C\cdot a\,^{k\,x} \) | \( C\cdot k\cdot a\,^{k\,x} \cdot \ln a \) |
| \( a\cdot f(x) \) | \( a\cdot f\,'(x) \) |
| \( f(x) + g(x)\, \) | \( f\,'(x) + g\,'(x) \) |
De två sista raderna i tabellen är snarare generella satser än deriveringsregler. De gäller för alla funktioner \( f(x)\, \) och \( g(x)\, \). Av praktiska skäl tar vi upp dem ändå i samma tabell som deriveringsreglerna. Denna tabell kommer att ytterligare kompletteras i Matte 4-kursen då vi kommer att lära oss fler deriveringsregler, speciellt regler för derivatan av en produkt resp. kvot av funktioner, den s.k. produkt- resp. kvotregeln.
Copyright © 2011-2016 Taifun Alishenas. All Rights Reserved.
