Skillnad mellan versioner av "1.2 Fördjupning till Faktorisering av Polynom"

Från Mathonline
Hoppa till: navigering, sök
m (→‎Det allmänna fallet (icke-normalform))
m
 
(201 mellanliggande versioner av samma användare visas inte)
Rad 1: Rad 1:
 +
__NOTOC__
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
−
{{Not selected tab|[[Repetition Faktorisering & Vieta från Matte 2|Repetition Faktorisering]]}}
+
{{Not selected tab|[[1.1 Polynom|<span style="color:blue"> <<&nbsp;&nbsp;Förra avsnitt</span>]]}}
−
{{Not selected tab|[[1.2 Faktorisering av polynom|Teori]]}}
+
{{Not selected tab|[[1.2 Faktorisering av polynom|Genomgång]]}}
 
{{Not selected tab|[[1.2 Övningar till Faktorisering av polynom|Övningar]]}}
 
{{Not selected tab|[[1.2 Övningar till Faktorisering av polynom|Övningar]]}}
 
{{Selected tab|[[1.2 Fördjupning till Faktorisering av Polynom|Fördjupning]]}}
 
{{Selected tab|[[1.2 Fördjupning till Faktorisering av Polynom|Fördjupning]]}}
−
{{Not selected tab|[[1.2 Internetlänkar till Faktorisering av Polynom|Internetlänkar]]}}
+
{{Not selected tab|[[1.3 Rationella uttryck|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
  
  
 +
<!-- [[Media: Lektion_4_Faktorisering_av_polynom_Ruta.pdf|<b><span style="color:blue">Lektion 4 Faktorisering av polynom</span></b>]]
  
−
[[Media: Lektion_4_Faktorisering_av_polynomF_Ruta.pdf|Lektion 4 Faktorisering av polynom: Fördjupning]]
+
[[Media: Lektion_5_Faktorisering_av_polynom_Ruta.pdf|<b><span style="color:blue">Lektion 5 Faktorisering av polynom: Fördjupning</span></b>]] -->
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; <div class="border-divblue">[[Media: Solving polynomial equations.pdf|<b>Intressant bredvidläsning: Solving polynomial equations</b>]]</div>
  
−
__TOC__
 
  
−
== Det allmänna fallet (icke-normalform) ==
+
== <b><span style="color:#931136">Faktorisering av 2:a gradspolynom (icke-normalform)</span></b> ==
 +
<big>
 +
Alla hittills i genomgången behandlade polynom var i normalform.
  
−
Alla våra hittills behandlade polynom var i normalform. Den s.k. ledande koefficienten, dvs den kvadratiska termens koefficient eller talet framför <math>x^2\,</math>, var alltid <math>1\,</math>. Det behöver inte alltid vara så.
+
Ett polynom är i <b><span style="color:red">normalform</span></b> om den ledande koefficienten <math>-</math> dvs den högsta potensens koefficient <math>-</math> är <math> \, 1 \,</math>.
  
−
Låt oss t.ex. faktorisera följande polynom med ledande koefficienten <math>3\,</math>:
+
Det behöver inte alltid vara så. Hur faktoriserar vi då?
 +
</big>
  
−
:::::::::<math> 3\,x^2 - 6\,x - 9 </math>
+
=== <b><span style="color:#931136">Exempel 1</span></b> ===
  
−
Lösningen består i att återföra problemet till den kända typen i normalform genom att bryta ut den ledande koefficienten:
+
<div class="ovnE">
 +
Faktorisera följande polynom (med ledande koefficienten <math> \,3\,</math>):
  
−
::::::<math> 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) </math>
+
:::::<math> 3\,x^2 - 6\,x - 9 </math>
  
−
Vi faktoriserar först det nya polynomet <math> x^2 - 2\,x - 3 </math> som är i normalform enligt:
+
Bryta ut den ledande koefficienten för att återföra problemet till den [[1.2_Faktorisering_av_polynom#Faktorisering_av_2:a_gradspolynom_.28normalform.29|<b><span style="color:blue">kända typen i normalform</span></b>]]:
  
−
::::::<math> x^2 - 2\,x - 3 = (x-x_1) \cdot (x-x_2) </math>
+
:::::<math> 3\,x^2 - 6\,x - 9\,=\,3 \cdot {\color{Red} {(x^2 - 2\,x - 3)}}\,=\,3 \cdot {\color{Red} {(x-x_1) \cdot (x-x_2)}}  </math>
  
−
Efter att ha löst detta nya problem kan vi gå tillbaka till det ursprungliga problemet för att få faktoriseringen av <math> 3\,x^2 - 6\,x - 9 </math>.
+
Faktorisera först polynomet <math> \; {\color{Red} {x^2 - 2\,x - 3}} \; </math> i normalform genom att bestämma dess nollställen<span style="color:black">:</span>
  
−
För att få fram <math> x_1\,</math> och <math> x_2\,</math> som ger oss faktoriseringen av <math> x^2 - 2\,x - 3 </math> kan vi som vanligt använda Vietas formler:
+
<math> \begin{array}{rrlcr} & \quad\; {\color{Red} {x^2 - 2\,x - 3}} & = \;\;\; 0    \\
 +
          {\rm Vieta:}    & \quad\;    x_1  +  x_2              & = -(-2) = 2  \\
 +
                            & \quad\;    x_1 \cdot x_2              & = -3
 +
      \end{array}</math>
  
−
::::::<math> \begin{align} x_1  +  x_2 & = -(-2) = 2  \\
+
::::::::<big><math> \Downarrow </math></big>
−
                      x_1 \cdot x_2 & = -3
+
−
            \end{align}</math>
+
  
−
Man hittar lösningarna <math> x_1 = 3\,</math> och <math> x_2 = -1\,</math> eftersom <math> 3 + (-1) = 2\,</math> och <math> 3 \cdot (-1) = -3 </math>.
+
<math> x_1 = 3\,</math> och <math> x_2 = -1\,</math> eftersom <math> 3 + (-1) = 2\,</math> och <math> 3 \cdot (-1) = -3 </math>  
  
−
Därför kan polynomet <math> x^2 - 2\,x - 3 </math> faktoriseras så här:
+
::::::::<big><math> \Downarrow </math></big>
  
−
::::::<math> x^2 - 2\,x - 3 = (x - 3) \cdot (x + 1) </math>
+
:::::<math> x^2 - 2\,x - 3 = (x - 3) \cdot (x + 1) </math>
  
−
Går vi tillbaka och sätter in denna lösning i det ursprungliga problemets ansats får vi det ursprungliga polynomets faktorisering:
+
Går vi tillbaka och sätter in denna lösning i det ursprungliga polynomet får vi faktoriseringen<span style="color:black">:</span>
  
−
::::::<math> 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) = 3\,(x-3) \cdot (x+1) </math>
+
:::::<math> 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) = 3\,(x-3) \cdot (x+1) </math>
 +
</div>
  
−
Den ovan beskrivna metoden fungerar alltid när 2:a gradspolynomet har ett eller två nollställen. Har det däremot inget nollställe alls finns det inte heller någon faktorisering.
 
  
−
==== Exempel ====
+
<big>
 +
Vad gör man om den ledande koefficienten "inte går att bryta ut" eftersom polynomets andra koefficienter inte går att dela jämnt med den ledande koefficienten?
 +
</big>
  
−
Vad gör man om den ledande koefficienten "inte går att bryta ut" eftersom den inte delar de andra koefficienterna jämnt? Man gör det ändå och går över till tal i bråkform. Det finns nämligen ingen begränsning varken för polynomets nollställen eller koefficienter, när det gäller taltypen: De kan vara heltal, som var fallet hittills i våra exempel, men även bråk- eller decimaltal. Låt oss t.ex. faktorisera följande polynom med en ledande koefficient som inte delar de andra koefficienterna jämnt:
 
  
−
:::::::::::::::::<math> 7\,x^2 - 5\,x - 2 </math>
+
=== <b><span style="color:#931136">Exempel 2</span></b> ===
  
−
Vi bryter ut 7 och skriver det nya polynomets koefficienter i bråkform:
+
<div class="ovnC">
 +
Faktorisera följande polynom vars koefficienter <math> \, 5 \, </math> och <math> \, 2 \, </math> inte går att dela jämnt med den ledande koefficient <math> \, 7 </math><span style="color:black">:</span>
  
−
::::::::::<math> 7\,x^2 - 5\,x - 2 = 7\,(x^2 - {5 \over 7}\,x - {2 \over 7}) = 7\,(x-x_1) \cdot (x-x_2) </math>
+
:::::<math> 7\,x^2 - 5\,x - 2 </math>
  
−
För att få fram <math> x_1\,</math> och <math> x_2\,</math> använder vi Vietas formler:
+
Vi bryter ut 7 genom att gå över till tal i bråkform<span style="color:black">:</span>
  
−
<math> \begin{align} x_1  +  x_2 & = {5 \over 7}  \\
+
:::::<math> 7\,x^2 - 5\,x - 2 = 7\,(x^2 - {5 \over 7}\,x - {2 \over 7}) = 7\,(x-x_1) \cdot (x-x_2) </math>
 +
 
 +
För att få fram <math> x_1\,</math> och <math> x_2\,</math> använder vi Vietas formler<span style="color:black">:</span>
 +
 
 +
:::::<math> \begin{align} x_1  +  x_2 & = {5 \over 7}  \\
 
                     x_1 \cdot x_2 & = - {2 \over 7}
 
                     x_1 \cdot x_2 & = - {2 \over 7}
 
         \end{align}</math>
 
         \end{align}</math>
  
−
Man hittar lösningarna <math> x_1 = 1\,</math> och <math> x_2 = -{2 \over 7}\,</math> eftersom <math> 1 - {2 \over 7} = {5 \over 7} </math> och <math> 1 \cdot {-2 \over 7} = {-2 \over 7} </math>.  
+
Man hittar lösningarna <math> \, x_1 = 1 \, </math> och <math> \displaystyle \, x_2 = -{2 \over 7} \, </math> eftersom <math> \displaystyle \, 1 - {2 \over 7} = {5 \over 7} \, </math> och <math> \displaystyle \, 1 \cdot (-{2 \over 7}) = -{2 \over 7} </math>.  
  
−
Så får vi det nya polynomets faktorisering:
+
Så får vi det nya polynomets faktorisering<span style="color:black">:</span>
  
−
<math> x^2 - {5 \over 7}\,x - {2 \over 7} = (x - 1) \cdot (x + {2 \over 7}) </math>
+
:::::<math> x^2 - {5 \over 7}\,x - {2 \over 7} = (x - 1) \cdot (x + {2 \over 7}) </math>
  
−
Går vi tillbaka och sätter in detta i det ursprungliga problemets ansats får vi det ursprungliga polynomets faktorisering:
+
Går vi tillbaka och sätter in detta i det ursprungliga problemets ansats får vi det ursprungliga polynomets faktorisering<span style="color:black">:</span>
  
−
::::::::::<math> 7\,x^2 - 5\,x - 2 = 7\,(x^2 - {5 \over 7}\,x - {2 \over 7}) = 7\,(x - 1) \cdot (x + {2 \over 7}) </math>
+
:::::<math> 7\,x^2 - 5\,x - 2 = 7\,(x^2 - {5 \over 7}\,x - {2 \over 7}) = 7\,(x - 1) \cdot (x + {2 \over 7}) </math>
  
−
Vill man i slutet bli av med bråktal kan man multiplicera in 7 i den andra parentesen och skriva faktoriseringen så här:
+
Vill man i slutet bli av med bråktal kan man multiplicera in 7 i den andra parentesen och skriva faktoriseringen så här<span style="color:black">:</span>
  
−
:::::::::::::<math> 7\,x^2 - 5\,x - 2 = (x - 1) \cdot (7\,x + 2) </math>
+
::::::::<math> 7\,x^2 - 5\,x - 2 = (x - 1) \cdot (7\,x + 2) </math>
 +
</div>
  
−
== Faktorisering av 3:e och högre gradspolynom ==
 
  
−
Faktorisering av 2:a gradspolynom är alltid möjlig för oss eftersom vi kan lösa 2:a gradsekvationer. I de fall man lyckas återföra 3:e eller högre gradsekvationer till 2:a gradsekvationer är det även möjligt att faktorisera polynom av högre grad än 2. Ett sådant fall föreligger om man antingen känner till eller t.ex. med hjälp av grafen kan få fram åtminstone en lösning till en 3:e gradsekvation. Låt oss genomföra detta för följande exempel:
+
<big>
 +
Faktorisering av 2:a gradspolynom är alltid möjlig för oss eftersom vi kan lösa 2:a gradsekvationer och beräkna nollställena.
  
−
'''Problem:''' Faktorisera 3:e gradspolynomet
+
I de fall man lyckas återföra 3:e eller högre gradsekvationer till 2:a gradsekvationer är det även möjligt att faktorisera polynom av högre grad än 2. 
 +
</big>
  
−
:::::::<math> P(x) = x^3 - 6\,x^2 + 5\,x + 12 </math>
 
  
−
'''Lösning:''' För att få fram något av polynomets nollställen ritar vi
+
== <b><span style="color:#931136">Faktorisering av 3:e och högre gradspolynom</span></b> ==
  
−
grafen till funktionen <math> y = x^3 - 6\,x^2 + 5\,x + 12 </math>
 
  
−
[[Image: 3e_gradspolynom_70.jpg]]
+
=== <b><span style="color:#931136">Exempel</span></b> ===
  
−
Grafen visar att polynomet har tre nollställen av vilka ett är ganska tydligt på bilden och kan avläsas till x = -1, medan de andra två är mindre tydliga. För att avgöra om detta nollställe är exakt gör vi en prövning genom att sätta in x = -1 i polynomet:
+
<div class="ovnA">
 +
<table>
 +
<tr> <td>
  
−
<math> P(-1) = (-1)^3 - 6\,\cdot\,(-1)^2 + 5\,\cdot\,(-1) + 12 = -1 - 6\,\cdot\,1 - 5 + 12 = -1 -6 -5 +12 = -12 +12 = 0 </math>
+
Faktorisera polynomet <math> \qquad P(x) \; = \; x^3 - 6\,x^2 + 5\,x + 12 </math>
  
−
Prövningen visar att x = -1 är ett exakt nollställe till P(x). Härav kan vi nu dra slutsatsen att de två andra nollställena måste uppfylla följande ekvation:
 
  
−
:::::::<math> P(x) = x^3 - 6\,x^2 + 5\,x + 12 = Q(x) \cdot (x+1) = 0 </math>
+
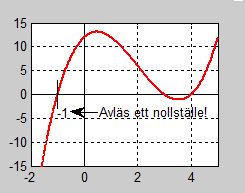
<b><span style="color:#931136">Lösning:</span></b> För att få fram ett av polynomets nollställen ritar vi grafen:
  
−
där <math> Q(x) </math> är ett 2:a gradspolynom som vi inte känner till än. Denna slutsats baseras på en generell matematisk sats, algebrans fundamentalsats som säger att ett polynom av grad n har n nollställen. Vi kan med nollproduktmetoden resonera så här: För att produkten <math> Q(x) \cdot (x+1) </math> ska vara lika med 0 måste antingen <math> Q(x) </math> eller <math> (x+1) </math> vara lika med 0. Vi vet redan att <math> (x+1) </math> är 0 för x = -1  som är <math> P(x) </math>:s ena nollställe. Alltså måste <math> P(x) </math>:s andra två nollställen finnas i <math> Q(x) </math>. Med andra ord de andra två nollställen måste vara det 2:a gradspolynomet <math> Q(x) </math>:s nollställen. Kan vi bestämma <math> Q(x) </math>, beräkna dess nollställen samt ställa upp dess faktorform, har vi faktoriserat även det 3:e gradspolynomet <math> P(x) </math>. Vi har ju redan hittat ett nollställe och ställt upp en ansats till faktoriseringen av <math> P(x) </math> i form av ekvationen ovan. Vi bearbetar nu vidare denna ansats genom att införa i den för <math> Q(x) </math> den allmänna formen för ett 2:a gradspolynom:
+
Grafen visar att polynomet har tre nollställen av vilka ett kan avläsas
  
−
<math> Q(x) = a\,x^2 + b\,x + c </math>
+
till <math> \, x_1 = -1 </math>. För att avgöra om detta nollställe är exakt gör vi en kon-
  
−
där a, b och c är koefficienter som vi måste bestämma. Sätter vi in denna form i ansasten ovan får vi:
+
troll genom att sätta in <math> \, x_1 = -1 \, </math> i polynomet:
 +
</td> <td><math> \quad </math></td> <td>[[Image: 3e_gradspolynom.jpg]]</td> </tr>
 +
</table>
 +
<math> P(-1) = (-1)^3 - 6\,\cdot\,(-1)^2 + 5\,\cdot\,(-1) + 12 = -1 - 6\,\cdot\,1 - 5 + 12 = -12 +12 = 0 </math>
  
−
::::::<math> x^3 - 6\,x^2 + 5\,x + 12 = (a\,x^2 + b\,x + c) \cdot (x+1) </math>
+
Kontrollen visar att <math> x_1 = -1\, </math> är ett exakt nollställe till <math> P(x) </math>. Slutsats: Faktorn <math> \, (x + 1) \, </math> kan brytas ut<span style="color:black">:</span>
  
−
Vi vet från förra avsnitt att två polynom är lika med varandra om alla deras motsvarande koefficienter, dvs de som tillhör termer av samma grad, överensstämmer. För att kunna genomföra denna jämförelse av koefficienter utvecklar vi produkten på höger sidan och ordnar termerna:
+
:::::<math> P(x) \; = \; x^3 - 6\,x^2 + 5\,x + 12 \; = \; Q(x) \cdot (x+1) \; = \; 0 </math>
 +
 
 +
där <math> \, Q(x) \, </math> är ett 2:a gradspolynom som vi inte känner till än, se [[1.2_Fördjupning_till_Faktorisering_av_Polynom#Algebrans_fundamentalsats|<b><span style="color:blue">algebrans fundamentalsats</span></b>]].
 +
 
 +
<math> P(x)\, </math>:s två andra nollställen måste vara det 2:a gradspolynomet <math> \, Q(x)\, </math>:s nollställen.
 +
 
 +
Vi bestämmer <math> \, Q(x)\, </math> genom att sätta den till den allmänna formen för 2:a gradspolynom<span style="color:black">:</span>
 +
 
 +
:::::<math> Q(x) = a\,x^2 + b\,x + c </math>
 +
 
 +
där <math> \, a, b, c \, </math> är koefficienter som vi måste bestämma. Sätter vi in denna form i ansasten ovan får vi:
 +
 
 +
:::::<math> x^3 - 6\,x^2 + 5\,x + 12 = (a\,x^2 + b\,x + c) \cdot (x+1) </math>
 +
 
 +
Vi bestämmer <math> \, a, b, c \, </math> genom lösa upp parentesen och jämföra koefficienterna<span style="color:black">:</span>
  
 
::<math> x^3 - 6\,x^2 + 5\,x + 12 = a\,x^3 + b\,x^2 + c\,x + a\,x^2 + b\,x + c = a\,x^3 + (b+a)\,x^2 + (c+b)\,x + c </math>
 
::<math> x^3 - 6\,x^2 + 5\,x + 12 = a\,x^3 + b\,x^2 + c\,x + a\,x^2 + b\,x + c = a\,x^3 + (b+a)\,x^2 + (c+b)\,x + c </math>
  
−
Jämförelse av koefficienterna på höger- och vänsterled ger:
+
[[1.1_Fördjupning_till_Polynom#J.C3.A4mf.C3.B6relse_av_koefficienter|<b><span style="color:blue">Jämförelse av koefficienterna</span></b>]] på höger- och vänsterled ger<span style="color:black">:</span>
  
−
::<math> \begin{align} a    & = 1    \\
+
:::::<math> \begin{align} a    & = 1    \\
 
                       b + a & = -6  \\
 
                       b + a & = -6  \\
 
                       c + b & = 5    \\
 
                       c + b & = 5    \\
Rad 123: Rad 154:
 
         \end{align}</math>
 
         \end{align}</math>
  
−
Genom insättning av <math> a = 1 </math> i den andra och <math> c = 12 </math> i den tredje ekvationen får vi i båda fall b = -7. Därmed har vi bestämt polynomet <math>Q(x)</math>:
+
Genom insättning av <math> \, a = 1 \, </math> i den andra och <math> \, c = 12 \, </math> i den tredje ekvationen får vi i båda fall <math> \, b = -7 \, </math>.
  
−
<math> Q(x) = x^2 - 7\,x + 12 </math>
+
Därmed har vi bestämt polynomet <math> \, Q(x) \, </math><span style="color:black">:</span>
  
−
I början av detta avsnitt (Faktorisering av 2:a gradspolynom) hade vi faktoriserat det här polynomet till:
+
:::::<math> Q(x) = x^2 - 7\,x + 12 </math>
  
−
::::::::<math> x^2 - 7\,x + 12 = (x-3) \cdot (x-4) </math>
+
I [[1.2_Faktorisering_av_polynom#Faktorisering_av_2:a_gradspolynom_.28normalform.29|<b><span style="color:blue">Faktorisering av 2:a gradspolynom</span></b>]] hade vi faktoriserat <math> \, Q(x) \, </math> så här<span style="color:black">:</span>
  
−
Inför vi nu detta resultat i vår ansats i början får vi faktoriseringen för P(x):
+
:::::<math> x^2 - 7\,x + 12 = (x-3) \cdot (x-4) </math>
  
−
::<math> P(x) = x^3 - 6\,x^2 + 5\,x + 12 = Q(x) \cdot (x+1) = (x^2 - 7\,x + 12) \cdot (x+1) = (x-3)\,\cdot\,(x-4)\,\cdot\,(x+1) </math>
+
där <math> \, x_2 = 3 \, </math> och <math> \, x_3 = 4 \, </math> är <math> \, Q(x)\, </math>:s nollställen.
  
−
Den ovan beskrivna metoden kan i princip även användas för faktorisering av polynom av högre grad än 3. Anledningen till det är algebrans fundamentalsats som vi redan nämnde tidigare och som lite förenklad lyder så här:
+
Inför vi nu detta resultat i vår ansats i början får vi den fullständiga faktoriseringen för <math> \, P(x) </math><span style="color:black">:</span>
  
−
== Algebrans fundamentalsats ==
+
<math> P(x) = x^3 - 6\,x^2 + 5\,x + 12 = Q(x) \cdot (x+1) = (x^2 - 7\,x + 12) \cdot (x+1) = \underline{(x-3)\,\cdot\,(x-4)\,\cdot\,(x+1)} </math>
 +
</div>
  
−
'''Sats''':
+
<big>
−
::::<big>Ett polynom av grad n har exakt n nollställen <math> x_1, \, x_2, \,\quad\ldots\, x_n </math>och kan faktoriseras så här:</big>
+
Den ovan beskrivna metoden kan i princip även användas för faktorisering av polynom av högre grad än 3.
  
−
:::<math> a_n \, x^n \,+\, a_{n-1} \, x^{n-1} + \quad \ldots \quad + a_1 \, x \,+\, a_0\;=\;a_n \cdot\, (x-x_1) \,\cdot\, (x-x_2) \,\cdot\quad\ldots\quad \cdot\, (x-x_n) </math>  
+
Till grund för alla dessa faktoriseringar ligger algebrans fundamentalsats som vi redan nämnde tidigare och som lite förenklad lyder så här:
 +
</big>
 +
 
 +
 
 +
== <b><span style="color:#931136">Algebrans fundamentalsats</span></b> ==
 +
 
 +
 
 +
<div class="border-divblue">
 +
<big>
 +
Ett polynom av grad <math> n\, </math> har exakt <math> n\, </math> komplexa nollställen <math> \; x_1, \, x_2, \,\ldots\, , x_n \; </math> och kan faktoriseras så här<span style="color:black">:</span>
 +
 
 +
<math> a_n \, x^n \,+\, a_{n-1} \, x^{n-1} + \quad \ldots \quad + a_1 \, x \,+\, a_0 \quad = \quad {\color{Red} {a_n \cdot\, (x-x_1) \,\cdot\, (x-x_2) \,\cdot\quad\ldots\quad \cdot\, (x-x_n)}} </math>  
 +
</big></div>
 +
 
 +
 
 +
<big>
 +
Se [http://www.lth.se/fileadmin/lth/student/Teknisk_matematik/Filer/Projektrapport/Matematisk_kommunikation/projekt-matkom06.pdf <b><span style="color:blue">bevis, historia & annat gott</span></b>].
 +
</big>
 +
 
 +
== Anmärkningar: ==
 +
 
 +
<big>
 +
*&nbsp;&nbsp;Fundamentalsatsens egentliga utsaga är: <b><span style="color:red">Ett polynom av grad <math> n\, </math> har exakt <math> n\, </math> komplexa nollställen.</span></b> Den ska tolkas så här:
 +
 
 +
*&nbsp;&nbsp;<b><span style="color:red">Antalet <math> n\, </math></span></b> borde räknas med <b><span style="color:red">multiplicitet</span></b>, dvs dubbla rötter är räknade två gånger, tredubbla tre gånger osv.
 +
 
 +
*&nbsp;&nbsp;Den fullständiga faktoriseringen i linjära faktorer <math> (x-x_i)\, </math> där <math> x_i\, </math> = polynomets nollställen, är endast möjlig i mängden av <b><span style="color:red">komplexa tal</span></b>.
 +
 
 +
*&nbsp;&nbsp;Räknar man endast med reella tal kommer vissa polynom att faktoriseras till linjära och kvadratiska faktorer, där de kvadratiska faktorerna har komplexa rötter.
 
----
 
----
−
Anmärkningar:
+
</big>
−
* Egentligen utgör endast den första delen (polynom av grad n har exakt n nollställen) algebrans fundamentalsats. Den andra delen om faktorisering är en följd av den.
+
−
* Antalet n nollställen är räknade med multiplicitet, dvs dubbla rötter är räknade två gånger, tredubbla tre gånger osv.
+
−
* Den fullständiga faktoriseringen i linjära faktorer <math> (x-x_i)\, </math> är endast möjlig i mängden av s.k. komplexa tal, en taltyp som inte behandlas i C-kursen. För oss som räknar med reella tal (största taltyp vi känner till) betyder der att vissa polynom endast kan faktoriseras till linjära och kvadratiska faktorer.
+
  
−
==== Exempel 1 ====
 
  
−
<math> P(x) = x^5 - 5\,x^4 + 17\,x^3 - 13\,x^2 = x\cdot x\cdot (x-1)\cdot (x^2 - 4\,x + 13) </math>
+
<div class="exempel12">
 +
=== <span style="color:#931136">Exempel 1</span> ===
  
−
Polynomet P(x) har en dubbelrot x = 0, en enkel rot x = 1 och två s.k. komplexa rötter som ger upphov till den kvadratiska faktor som står sist. För oss räcker det att ange faktoriseringen i forman ovan. Vi kan få fram den med de metoder vi lärt oss i detta avsnitt: Den dubbla roten x = 0 får vi genom att bryta ut <math> x^2 </math>, roten x = 1 kan vi t.ex. få via grafen samt en prövning. Den kvadratiska faktorns koefficienter kan vi beräkna med hjälp av jämförelse av koefficienter. Att det inte går att få fram en fullständig faktorisering i linjära faktorer beror på att den kvadratiska faktorn saknar reella rötter.
+
Faktorisera följande polynom fullständigt<span style="color:black">:</span>
  
−
==== Exempel 2 ====
+
<math> P(x) = x^4 - 29\;x^2 + 100 </math>
  
−
Att vi ändå kan ha praktisk nytta av algebrans fundamentalsats visar följande exempel: I [[1.1 Övning 6|övning 6]] i avsnittet 1.1 Ekvationer hade vi (förhoppningsvis) löst 4:e gradsekvationen
+
I [[Övningar till Rotekvationer och högre gradsekvationer#Övning 6|<b><span style="color:blue">övning 6</span></b>]] till repetitionsavsnittet [[Ekvationer|<b><span style="color:blue">Ekvationer</span></b>]] hade vi löst 4:e gradsekvationen
  
 
<math> x^4 - 29\;x^2 = -100 </math>  
 
<math> x^4 - 29\;x^2 = -100 </math>  
Rad 169: Rad 226:
 
<math> P(x) = x^4 - 29\;x^2 + 100 = 0 </math>  
 
<math> P(x) = x^4 - 29\;x^2 + 100 = 0 </math>  
  
−
Pga kännedomen om ekvationens lösningar som är identiska med polynomets nollställen, kan vi enligt algebrans fundamentalsats faktorisera 4:e gradspolynomet P(x) så här:
+
Pga kännedomen om ekvationens lösningar som är identiska med polynomets nollställen, kan vi enligt algebrans fundamentalsats faktorisera 4:e gradspolynomet <math> P(x)\, </math> så här:
  
 
<math> P(x) = x^4 - 29\;x^2 + 100 = (x-5) \cdot (x+5) \cdot (x-2) \cdot (x+2) </math>
 
<math> P(x) = x^4 - 29\;x^2 + 100 = (x-5) \cdot (x+5) \cdot (x-2) \cdot (x+2) </math>
 +
</div>
 +
 +
 +
<div class="exempel12">
 +
=== <span style="color:#931136">Exempel 2</span> ===
 +
 +
Faktorisera polynomet <math> P(x)\, </math> fullständigt när följande delfaktorisering redan existerar<span style="color:black">:</span>
 +
 +
::<math> P(x) = x^5 - 5\,x^4 + 17\,x^3 - 13\,x^2 = x\cdot x\cdot (x-1)\cdot (x^2 - 4\,x + 13) </math>
 +
 +
Delfaktoriseringen visar en dubbelrot <math> x = 0\, </math> och en enkel rot <math> x = 1\, </math>. Man kan få fram den med de metoder vi lärt oss i detta avsnitt: Den dubbla roten <math> x = 0\, </math> får man genom att bryta ut <math> x^2 </math>. Den enkla roten <math> x = 1\, </math> kan man få via grafen samt en prövning. Den sista faktorn kan beräknas med hjälp av jämförelse av koefficienter. Denna delfaktorisering stannar inom ramen av de reella talen.
 +
 +
Enligt algebrans fundamentalsats måste 5:e gradspolynomet <math> P(x)\, </math> ha två rötter till som ger upphov till den kvadratiska faktorn <math> x^2 - 4\,x + 13 </math> som står sist.
 +
 +
Vill man gå vidare och få fram den fullständiga faktoriseringen i linjära faktorer måste även den kvadratiska faktorn faktoriseras. Detta innebär att vi måste beräkna dess rötter som visar sig vara komplexa<span style="color:black">:</span>
 +
 +
::::::<math>\begin{array}{rcl} x^2 - 4\,x + 13 & = & 0                            \\
 +
                                      x_{1,2} & = & 2 \pm \sqrt{4 - 13}          \\
 +
                                      x_{1,2} & = & 2 \pm \sqrt{-9}              \\
 +
                                      x_{1,2} & = & 2 \pm \sqrt{9 \cdot (-1)}    \\
 +
                                      x_{1,2} & = & 2 \pm \sqrt{9}\cdot \sqrt{-1} \\
 +
                                      x_1    & = & 2 + 3\,i                      \\
 +
                                      x_2    & = & 2 - 3\,i                      \\
 +
            \end{array}</math>
 +
 +
Vi får alltså följande faktorisering av den kvadratiska faktorn:
 +
 +
::<math> x^2 - 4\,x + 13  = (x - (2+3\,i)) \cdot (x - (2-3\,i)) = (x - 2-3\,i) \cdot (x - 2+3\,i)</math>
 +
 +
Därmed blir den fullständiga faktoriseringen av polynomet <math> P(x)\, </math> i linjära faktorer:
 +
 +
<math> P(x) = x^5 - 5\,x^4 + 17\,x^3 - 13\,x^2 = x\cdot x\cdot (x-1)\cdot (x - 2-3\,i) \cdot (x - 2+3\,i) </math>
 +
 +
Dvs <math> P(x)\, </math> har förutom dubbelroten <math> x = 0\, </math> och den enkla roten <math> x = 1\, </math> även de två komplexa rötterna <math> x = 2 + 3\,i </math> och <math> x = 2 - 3\,i </math>. Sammanlagt har 5:e gradspolynomet <math> P(x)\, </math> exakt 5 rötter, om man räknar rötterna med multiplicitet, dvs den dubbla rotter dubbelt och beräknar även de komplexa rötterna - i enlighet med algebrans fundamentalsats.
 +
</div>
 +
 +
 +
 +
  
  
  
−
[[Matte:Copyrights|Copyright]] © 2011-2014 Taifun Alishenas. All Rights Reserved.
+
[[Matte:Copyrights|Copyright]] © 2022 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved.

Nuvarande version från 3 februari 2022 kl. 13.27

        <<  Förra avsnitt          Genomgång          Övningar          Fördjupning          Nästa avsnitt  >>      


      
Intressant bredvidläsning: Solving polynomial equations


Faktorisering av 2:a gradspolynom (icke-normalform)

Alla hittills i genomgången behandlade polynom var i normalform.

Ett polynom är i normalform om den ledande koefficienten \(-\) dvs den högsta potensens koefficient \(-\) är \( \, 1 \,\).

Det behöver inte alltid vara så. Hur faktoriserar vi då?

Exempel 1

Faktorisera följande polynom (med ledande koefficienten \( \,3\,\)):

\[ 3\,x^2 - 6\,x - 9 \]

Bryta ut den ledande koefficienten för att återföra problemet till den kända typen i normalform:

\[ 3\,x^2 - 6\,x - 9\,=\,3 \cdot {\color{Red} {(x^2 - 2\,x - 3)}}\,=\,3 \cdot {\color{Red} {(x-x_1) \cdot (x-x_2)}} \]

Faktorisera först polynomet \( \; {\color{Red} {x^2 - 2\,x - 3}} \; \) i normalform genom att bestämma dess nollställen:

\( \begin{array}{rrlcr} & \quad\; {\color{Red} {x^2 - 2\,x - 3}} & = \;\;\; 0 \\ {\rm Vieta:} & \quad\; x_1 + x_2 & = -(-2) = 2 \\ & \quad\; x_1 \cdot x_2 & = -3 \end{array}\)

\( \Downarrow \)

\( x_1 = 3\,\) och \( x_2 = -1\,\) eftersom \( 3 + (-1) = 2\,\) och \( 3 \cdot (-1) = -3 \)

\( \Downarrow \)
\[ x^2 - 2\,x - 3 = (x - 3) \cdot (x + 1) \]

Går vi tillbaka och sätter in denna lösning i det ursprungliga polynomet får vi faktoriseringen:

\[ 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) = 3\,(x-3) \cdot (x+1) \]


Vad gör man om den ledande koefficienten "inte går att bryta ut" eftersom polynomets andra koefficienter inte går att dela jämnt med den ledande koefficienten?


Exempel 2

Faktorisera följande polynom vars koefficienter \( \, 5 \, \) och \( \, 2 \, \) inte går att dela jämnt med den ledande koefficient \( \, 7 \):

\[ 7\,x^2 - 5\,x - 2 \]

Vi bryter ut 7 genom att gå över till tal i bråkform:

\[ 7\,x^2 - 5\,x - 2 = 7\,(x^2 - {5 \over 7}\,x - {2 \over 7}) = 7\,(x-x_1) \cdot (x-x_2) \]

För att få fram \( x_1\,\) och \( x_2\,\) använder vi Vietas formler:

\[ \begin{align} x_1 + x_2 & = {5 \over 7} \\ x_1 \cdot x_2 & = - {2 \over 7} \end{align}\]

Man hittar lösningarna \( \, x_1 = 1 \, \) och \( \displaystyle \, x_2 = -{2 \over 7} \, \) eftersom \( \displaystyle \, 1 - {2 \over 7} = {5 \over 7} \, \) och \( \displaystyle \, 1 \cdot (-{2 \over 7}) = -{2 \over 7} \).

Så får vi det nya polynomets faktorisering:

\[ x^2 - {5 \over 7}\,x - {2 \over 7} = (x - 1) \cdot (x + {2 \over 7}) \]

Går vi tillbaka och sätter in detta i det ursprungliga problemets ansats får vi det ursprungliga polynomets faktorisering:

\[ 7\,x^2 - 5\,x - 2 = 7\,(x^2 - {5 \over 7}\,x - {2 \over 7}) = 7\,(x - 1) \cdot (x + {2 \over 7}) \]

Vill man i slutet bli av med bråktal kan man multiplicera in 7 i den andra parentesen och skriva faktoriseringen så här:

\[ 7\,x^2 - 5\,x - 2 = (x - 1) \cdot (7\,x + 2) \]


Faktorisering av 2:a gradspolynom är alltid möjlig för oss eftersom vi kan lösa 2:a gradsekvationer och beräkna nollställena.

I de fall man lyckas återföra 3:e eller högre gradsekvationer till 2:a gradsekvationer är det även möjligt att faktorisera polynom av högre grad än 2.


Faktorisering av 3:e och högre gradspolynom

Exempel

Faktorisera polynomet \( \qquad P(x) \; = \; x^3 - 6\,x^2 + 5\,x + 12 \)


Lösning: För att få fram ett av polynomets nollställen ritar vi grafen:

Grafen visar att polynomet har tre nollställen av vilka ett kan avläsas

till \( \, x_1 = -1 \). För att avgöra om detta nollställe är exakt gör vi en kon-

troll genom att sätta in \( \, x_1 = -1 \, \) i polynomet:

\( \quad \) 3e gradspolynom.jpg

\( P(-1) = (-1)^3 - 6\,\cdot\,(-1)^2 + 5\,\cdot\,(-1) + 12 = -1 - 6\,\cdot\,1 - 5 + 12 = -12 +12 = 0 \)

Kontrollen visar att \( x_1 = -1\, \) är ett exakt nollställe till \( P(x) \). Slutsats: Faktorn \( \, (x + 1) \, \) kan brytas ut:

\[ P(x) \; = \; x^3 - 6\,x^2 + 5\,x + 12 \; = \; Q(x) \cdot (x+1) \; = \; 0 \]

där \( \, Q(x) \, \) är ett 2:a gradspolynom som vi inte känner till än, se algebrans fundamentalsats.

\( P(x)\, \):s två andra nollställen måste vara det 2:a gradspolynomet \( \, Q(x)\, \):s nollställen.

Vi bestämmer \( \, Q(x)\, \) genom att sätta den till den allmänna formen för 2:a gradspolynom:

\[ Q(x) = a\,x^2 + b\,x + c \]

där \( \, a, b, c \, \) är koefficienter som vi måste bestämma. Sätter vi in denna form i ansasten ovan får vi:

\[ x^3 - 6\,x^2 + 5\,x + 12 = (a\,x^2 + b\,x + c) \cdot (x+1) \]

Vi bestämmer \( \, a, b, c \, \) genom lösa upp parentesen och jämföra koefficienterna:

\[ x^3 - 6\,x^2 + 5\,x + 12 = a\,x^3 + b\,x^2 + c\,x + a\,x^2 + b\,x + c = a\,x^3 + (b+a)\,x^2 + (c+b)\,x + c \]

Jämförelse av koefficienterna på höger- och vänsterled ger:

\[ \begin{align} a & = 1 \\ b + a & = -6 \\ c + b & = 5 \\ c & = 12 \end{align}\]

Genom insättning av \( \, a = 1 \, \) i den andra och \( \, c = 12 \, \) i den tredje ekvationen får vi i båda fall \( \, b = -7 \, \).

Därmed har vi bestämt polynomet \( \, Q(x) \, \):

\[ Q(x) = x^2 - 7\,x + 12 \]

I Faktorisering av 2:a gradspolynom hade vi faktoriserat \( \, Q(x) \, \) så här:

\[ x^2 - 7\,x + 12 = (x-3) \cdot (x-4) \]

där \( \, x_2 = 3 \, \) och \( \, x_3 = 4 \, \) är \( \, Q(x)\, \):s nollställen.

Inför vi nu detta resultat i vår ansats i början får vi den fullständiga faktoriseringen för \( \, P(x) \):

\( P(x) = x^3 - 6\,x^2 + 5\,x + 12 = Q(x) \cdot (x+1) = (x^2 - 7\,x + 12) \cdot (x+1) = \underline{(x-3)\,\cdot\,(x-4)\,\cdot\,(x+1)} \)

Den ovan beskrivna metoden kan i princip även användas för faktorisering av polynom av högre grad än 3.

Till grund för alla dessa faktoriseringar ligger algebrans fundamentalsats som vi redan nämnde tidigare och som lite förenklad lyder så här:


Algebrans fundamentalsats

Ett polynom av grad \( n\, \) har exakt \( n\, \) komplexa nollställen \( \; x_1, \, x_2, \,\ldots\, , x_n \; \) och kan faktoriseras så här:

\( a_n \, x^n \,+\, a_{n-1} \, x^{n-1} + \quad \ldots \quad + a_1 \, x \,+\, a_0 \quad = \quad {\color{Red} {a_n \cdot\, (x-x_1) \,\cdot\, (x-x_2) \,\cdot\quad\ldots\quad \cdot\, (x-x_n)}} \)


Se bevis, historia & annat gott.

Anmärkningar:

  •   Fundamentalsatsens egentliga utsaga är: Ett polynom av grad \( n\, \) har exakt \( n\, \) komplexa nollställen. Den ska tolkas så här:
  •   Antalet \( n\, \) borde räknas med multiplicitet, dvs dubbla rötter är räknade två gånger, tredubbla tre gånger osv.
  •   Den fullständiga faktoriseringen i linjära faktorer \( (x-x_i)\, \) där \( x_i\, \) = polynomets nollställen, är endast möjlig i mängden av komplexa tal.
  •   Räknar man endast med reella tal kommer vissa polynom att faktoriseras till linjära och kvadratiska faktorer, där de kvadratiska faktorerna har komplexa rötter.


Exempel 1

Faktorisera följande polynom fullständigt:

\( P(x) = x^4 - 29\;x^2 + 100 \)

I övning 6 till repetitionsavsnittet Ekvationer hade vi löst 4:e gradsekvationen

\( x^4 - 29\;x^2 = -100 \)

och fått lösningarna

\( x_1 = 5, \qquad x_2 = -5, \qquad x_3 = 2 \quad {\rm och} \quad x_4 = -2 \)

Vi kan skriva ekvationen som en polynomekvation

\( P(x) = x^4 - 29\;x^2 + 100 = 0 \)

Pga kännedomen om ekvationens lösningar som är identiska med polynomets nollställen, kan vi enligt algebrans fundamentalsats faktorisera 4:e gradspolynomet \( P(x)\, \) så här\[ P(x) = x^4 - 29\;x^2 + 100 = (x-5) \cdot (x+5) \cdot (x-2) \cdot (x+2) \]


Exempel 2

Faktorisera polynomet \( P(x)\, \) fullständigt när följande delfaktorisering redan existerar:

\[ P(x) = x^5 - 5\,x^4 + 17\,x^3 - 13\,x^2 = x\cdot x\cdot (x-1)\cdot (x^2 - 4\,x + 13) \]

Delfaktoriseringen visar en dubbelrot \( x = 0\, \) och en enkel rot \( x = 1\, \). Man kan få fram den med de metoder vi lärt oss i detta avsnitt: Den dubbla roten \( x = 0\, \) får man genom att bryta ut \( x^2 \). Den enkla roten \( x = 1\, \) kan man få via grafen samt en prövning. Den sista faktorn kan beräknas med hjälp av jämförelse av koefficienter. Denna delfaktorisering stannar inom ramen av de reella talen.

Enligt algebrans fundamentalsats måste 5:e gradspolynomet \( P(x)\, \) ha två rötter till som ger upphov till den kvadratiska faktorn \( x^2 - 4\,x + 13 \) som står sist.

Vill man gå vidare och få fram den fullständiga faktoriseringen i linjära faktorer måste även den kvadratiska faktorn faktoriseras. Detta innebär att vi måste beräkna dess rötter som visar sig vara komplexa:

\[\begin{array}{rcl} x^2 - 4\,x + 13 & = & 0 \\ x_{1,2} & = & 2 \pm \sqrt{4 - 13} \\ x_{1,2} & = & 2 \pm \sqrt{-9} \\ x_{1,2} & = & 2 \pm \sqrt{9 \cdot (-1)} \\ x_{1,2} & = & 2 \pm \sqrt{9}\cdot \sqrt{-1} \\ x_1 & = & 2 + 3\,i \\ x_2 & = & 2 - 3\,i \\ \end{array}\]

Vi får alltså följande faktorisering av den kvadratiska faktorn:

\[ x^2 - 4\,x + 13 = (x - (2+3\,i)) \cdot (x - (2-3\,i)) = (x - 2-3\,i) \cdot (x - 2+3\,i)\]

Därmed blir den fullständiga faktoriseringen av polynomet \( P(x)\, \) i linjära faktorer\[ P(x) = x^5 - 5\,x^4 + 17\,x^3 - 13\,x^2 = x\cdot x\cdot (x-1)\cdot (x - 2-3\,i) \cdot (x - 2+3\,i) \]

Dvs \( P(x)\, \) har förutom dubbelroten \( x = 0\, \) och den enkla roten \( x = 1\, \) även de två komplexa rötterna \( x = 2 + 3\,i \) och \( x = 2 - 3\,i \). Sammanlagt har 5:e gradspolynomet \( P(x)\, \) exakt 5 rötter, om man räknar rötterna med multiplicitet, dvs den dubbla rotter dubbelt och beräknar även de komplexa rötterna - i enlighet med algebrans fundamentalsats.




Copyright © 2022 TechPages AB. All Rights Reserved.

Hämtad från "https://matte3c.mathonline.se/index.php?title=1.2_Fördjupning_till_Faktorisering_av_Polynom&oldid=36783"