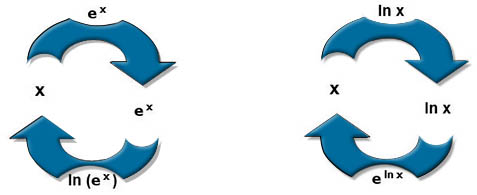Skillnad mellan versioner av "1.4 Talet e och den naturliga logaritmen"

Från Mathonline
Hoppa till: navigering, sök
m
m
 
(507 mellanliggande versioner av samma användare visas inte)
Rad 1: Rad 1:
 +
__NOTOC__
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
−
{{Not selected tab|[[1.3 Rationella uttryck|<-- Förra avsnitt]]}}
+
{{Not selected tab|[[1.3 Rationella uttryck| <<&nbsp;&nbsp;Förra avsnitt]]}}
−
{{Not selected tab|[[1.4 Repetition Exponentialfunktioner & logaritmer|Repetition: Exp. fkt. & logaritmer]]}}
+
{{Not selected tab|[[Repetition: 10-logaritmer|Rep.: 10-logaritmer]]}}
 
{{Selected tab|[[1.4 Talet e och den naturliga logaritmen|Genomgång]]}}
 
{{Selected tab|[[1.4 Talet e och den naturliga logaritmen|Genomgång]]}}
 
{{Not selected tab|[[1.4 Övningar till Talet e och den naturliga logaritmen|Övningar]]}}
 
{{Not selected tab|[[1.4 Övningar till Talet e och den naturliga logaritmen|Övningar]]}}
−
{{Not selected tab|[[1.5 Kontinuerliga och diskreta funktioner|Nästa avsnitt -->]]}}
+
{{Not selected tab|[[1.5 Kontinuerliga och diskreta funktioner|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 +
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 +
|}
 +
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 +
| style="border-bottom:1px solid #797979" width="5px" | &nbsp;
 +
{{Not selected tab|[[Repetition: Exponentialfunktioner|Rep.: Exponentialfunktioner]]}}
 +
{{Not selected tab|[[Repetition: Logaritmlagarna|Rep.: Logaritmlagarna]]}}
 +
{{Not selected tab|[[1.4 Talet e och den naturliga logaritmen|<span style="color:white">Genomgång</span>]]}}
 +
{{Not selected tab|[[1.4 Övningar till Talet e och den naturliga logaritmen|<span style="color:white">Övningar</span>]]}}
 +
{{Not selected tab|[[1.5 Kontinuerliga och diskreta funktioner|<span style="color:white">Nästa avsnitt&nbsp;&nbsp;>> </span>]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
  
−
[[Media: Lektion 8 Talet e Ruta.pdf|<strong><span style="color:blue">Lektion 8 Talet <math>\,e</math> och den naturliga logaritmen</span></strong>]]
 
−
__NOTOC__
 
−
<div class="ovnE">
 
−
=== <b><span style="color:#931136">Talet &nbsp;<big><math> e \,</math></big></span></b> ===
 
  
−
Ta fram din miniräknare, leta efter följande funktionsknapp och tryck på den:
+
<!-- [[Media: Lektion 9 Talet e Ruta.pdf|<b><span style="color:blue">Lektion 9 Talet <math>\,e</math> och den naturliga logaritmen</span></b>]] -->
  
−
::::::::::<big><big><math> e^{\,x} </math></big></big>
+
== <b><span style="color:#931136">Talet &nbsp;<big><math> e \,</math></big></span></b> ==
  
−
Mata in <math> 1 \, </math> och stäng parentesen. Nu borde det stå <math> \; {\bf e} </math> <span style="color:black">''^''</span> <math>(1) \; </math> i displayen.
+
<div class="ovnE">
 +
<big><b><span style="color:#931136">Experiment 1</span></b></big> <math> \qquad </math> Ta fram din miniräknare och gör så här:
  
−
Tryck på ENTER så får du:
+
# Leta efter funktionsknappen (ev. med hjälp av 2nd-knappen)<span style="color:black"></span> <big><math> \quad \boxed{e^{\,x}} \;\; </math></big>
 +
# Tryck på den, mata in <math> \, 1 \, </math> och stäng parentesen.
 +
# Tryck på ENTER när det står <big><math> \, e </math></big> <span style="color:black">''^''</span> <math>(1) \; </math> i räknarens display.
  
−
::::::::<big><math> 2,718281828\cdots </math></big>
+
Du har beräknat <big><math> \; e{\,^1} \; </math></big> eller <b><span style="color:blue">talet</span></b> <big><math> \, \color{blue} e \,</math></big>, dvs <math> \qquad 2,718281828\ldots \quad </math>,
  
−
Du har beräknat &nbsp; <big><math> e{\,^1} \,</math></big> eller [http://www.mathsisfun.com/numbers/e-eulers-number.html <strong><span style="color:blue">talet</span></strong> <big><math> {\color{Blue} e} </math></big>], en av matematikens mest kända konstanter, [https://sv.wikipedia.org/wiki/E_(tal) <strong><span style="color:blue">Eulers tal</span></strong>].
+
en av matematikens mest kända konstanter, även kallad [http://sv.wikipedia.org/wiki/E_(tal) <b><span style="color:blue">Eulers tal</span></b>].
−
 
+
−
Talet är  kallat efter den schweiziske matematikern [http://sv.wikipedia.org/wiki/Leonhard_Euler <strong><span style="color:blue">Leonard Euler</span></strong>] som levde på 1700-talet.
+
−
 
+
−
Det var han som ställde upp formler för beräkningen av detta märkliga tal.
+
 
</div>
 
</div>
  
  
 
<big>
 
<big>
−
Märkligt, därför att <big><math> \, e \,</math></big> inte ett rationellt tal, dvs det kan inte skrivas som ett bråk (kvot mellan två heltal), precis som talen <math> \pi,\, \sqrt{2},\, \sqrt{3},\,\cdots </math>. Sådana tal kallas <strong><span style="color:red">irrationella</span></strong>. Anledningen till att de inte kan skrivas som kvoter mellan två heltal är att de har oändligt många decimaler utan något som helst mönster som upprepas (period). Detta kan man själv övertyga sig om genom att beskåda de [http://apod.nasa.gov/htmltest/gifcity/e.5mil <strong><span style="color:blue">första 5 miljoner decimaler av talet <big><math> e \,</math></big></span></strong>].
+
Talet [http://www.mathsisfun.com/numbers/e-eulers-number.html <big><math> \, \color{blue} e \, </math></big>] är kallat efter den tysk-schweiziske matematikern [http://sv.wikipedia.org/wiki/Leonhard_Euler <b><span style="color:blue">Leonard Euler</span></b>] som på 1700-talet definierade detta märkliga tal.
  
−
Talet <big><math> e \,</math></big> förekommer bl.a. i en formel som enligt många är en av matematikens vackraste, nämligen sambandet mellan heltalet <math> 1\, </math>, de irrationella talen <big><math> e,\;\pi </math></big> och den s.k. imaginära eneheten <big><math> i\, </math></big>:
+
Märkligt, därför att <big><math> \, e \, </math></big> inte är ett "vanligt" tal som heltal eller bråk. Det är inte ett rationellt tal, se [http://mathonline.se:1800/index.php/1.1_Om_tal#Olika_typer_av_tal <b><span style="color:blue">olika typer av tal</span></b>].
  
−
:::::::::::<big><big><math> e^{\,2\,\pi\,i} </math></big> <math> = 1 </math></big>
+
Talet <big><math> \, e \, </math></big> är ett <b><span style="color:red">irrationellt tal</span></b>, precis som talen <math> \pi,\, \sqrt{2},\, \sqrt{3},\,\ldots \, </math>, som inte kan skrivas i bråkform.
  
 +
Irrationella tal är decimaltal som har en [http://mathonline.se:1800/index.php/1.3_Decimaltal#Icke-periodisk_decimalutveckling <b><span style="color:blue">icke-periodisk decimalutveckling</span></b>] dvs oändligt många decimaler utan något upprepande mönster (period). 
  
−
Ingen fara, vi har inte för avsikt att närmare gå in på denna komplexa formel. Vi nämner den bara för att illustrera betydelsen av talet <math> e \,</math>.
+
Här kan man beskåda de första <b><span style="color:blue">5 miljoner decimaler av talet</span></b> [http://apod.nasa.gov/htmltest/gifcity/e.5mil <b><span style="color:blue"><big><math> \, e \, </math></big></span></b>]. Leta gärna efter ett upprepande mönster! Du kommer inte att hitta något.
  
−
Ytterligare ett tecken på betydelsen av talet <math> e \,</math> är de otaliga natur- och ekonomiska lagar som formuleras med hjälp av den s.k. <strong><span style="color:red">exponentialfunktionen</span></strong> <big><math> {\color{Red} {y = e{\,^x}}} </math></big> som i sin tur ger upphov till sin invers, den s.k. <strong><span style="color:red">naturliga logaritmen</span></strong> <math> {\color{Red} {y = \ln x}} </math>, logaritmen med basen <big><math> e \, - </math></big> ett alternativ till 10-logaritmen med basen 10 som vi använt i Matte 2.  
+
<div class="border-divblue">
 +
&nbsp; <b><span style="color:#931136">OBS!</span></b> <math> \quad e \; </math> <small> är ingen variabel utan en s.k. <b><span style="color:red">namngiven konstant</span></b> som har värdet <math> \, 2,718281828\ldots \, </math>.</small></div>
 +
 
 +
Talet <big><math> \, e \, </math></big> förekommer bl.a. i en formel som enligt många är en av matematikens vackraste, nämligen sambandet mellan heltalet <math> 1\, </math>, de irrationella talen <big><math> e,\;\pi </math></big> och den imaginära enheten <math> \, i = \sqrt{-1} </math>, där även <big><math> \pi </math></big> och <big><math> \, i \, </math></big> är namngivna konstanter<span style="color:black">:</span>
 +
 
 +
::::::::::::::<big><big><math> e^{\,2\,\pi\,i} </math></big> <math> = 1 </math></big>
 +
 
 +
Ingen fara, vi har inte för avsikt att närmare gå in på denna formel. Vi nämner den bara för att illustrera betydelsen av talet <big><math> \, e \, </math></big> inom den [http://sv.wikipedia.org/wiki/Matematisk_analys <b><span style="color:blue">matematiska analysen</span></b>], den delen av matematiken som behandlar [[2.3_Gränsvärde|<b><span style="color:blue">gränsvärden</span></b>]], [[Matte_3_Kapitel_2_Derivata|<b><span style="color:blue">derivator</span></b>]], [[Matte_3_Kapitel_4_Integraler|<b><span style="color:blue">integraler</span></b>]] och differentialekvationer.
 
</big>
 
</big>
  
Rad 50: Rad 63:
 
<big>
 
<big>
  
−
Det enklaste sättet att beräkna talet <big><math> e \,</math></big> är att ta fram din räknare och <big><math> - </math></big> precis som det beskrevs inledningsvis <big><math> - </math></big> beräkna funktionen <big><math> e^{\,x} </math></big>:s värde för <math> x=1 \, </math> dvs beräkna <math> e^1\, </math> . Om man nöjer sig med detta är det o.k. Men om man vill veta <b>hur</b> värdet kommer till, kan man använda en av de formler Euler har bevisat:
+
<b><span style="color:red">Eulers formel</span></b> kan användas för att numeriskt få fram några decimaler av talet <b><span style="color:blue"><big><math> e \,</math></big></span></b>:
 +
<!-- som kommer att bevisas [[2.6_Derivatan_av_exponentialfunktioner#Eulers_bevis|<b><span style="color:blue">senare</span></b>]], -->
 +
::::<big><math> \left(1 + {1 \over n}\right)^n \to \; e </math></big> <math> \quad {\rm när} \quad n \to \infty </math>
  
−
:::::::::<math> \left(1 + {1 \over x}\right)^x \to e \quad {\rm när} \quad x \to \infty </math>
+
Dvs: Uttrycket ovan går mot <big><math> e \,</math></big> när <math> n\, </math> går mot oändligheten (<math> \infty </math>) eller:
  
−
Det betyder: Uttrycket ovan går mot <big><math> e \,</math></big> när <math> x\, </math> går mot oändligheten (<math> \infty </math>). Detta innebär att uttrycket närmar sig allt mer talet <big><math> e \,</math></big> ju större värden <math> x\, </math> antar. Tabellen nedan visar denna process:
+
Uttrycket närmar sig allt mer <big><math> \, e \,</math></big> ju större <math> \, n\, </math> blir. Tabellen tar några steg i denna process:
−
::::::::{| class="wikitable"
+
 
−
|-
+
<div class="border-divblue"><small>
−
! <math> x\, </math> || <math> \left(1 + {1 \over x}\right)^x </math>
+
{| class="wikitable"
−
|-
+
−
| align=left| <math> 1\,000 </math> ||align=left| <math> {\color{Red} {2,71}}6923932\cdots </math>
+
 
|-
 
|-
−
| align=left| <math> 10\,000 </math> ||align=left| <math> {\color{Red} {2,718}}145927\cdots </math>
+
| align=center|<math> n </math> || align=center|<math> 1\,000 </math> || align=center|<math> 1000\,000 </math> || align=center|<math> 1000\,000\,000 </math> || align=center|<math> 10\,000\,000\,000 </math> || align=center|<math> \to \infty </math>
 
|-
 
|-
−
| align=left| <math> 100\,000 </math> ||align=left| <math> {\color{Red} {2,7182}}68237\cdots </math>
+
!  align=center| <math> \left(1 + {1 \over n}\right)^n </math> || align=center|<math> {\color{Red} {2,71}}6923932\ldots </math> || <math> {\color{Red} {2,71828}}0469\ldots </math> || align=center|<math> {\color{Red} {2,71828182}}7\ldots </math> || align=center|<math> {\color{Red} {2,718281828\ldots}} </math> || align=center|<math> \quad \to \; {\color{Red} {{\rm Eulers\;tal\;} e}} \quad </math>
−
|-
+
−
| align=left| <math> 1000\,000 </math> ||align=left| <math> {\color{Red} {2,71828}}0469\cdots </math>  
+
−
|-
+
−
| align=left| <math> 10\,000\,000 </math> ||align=left| <math> {\color{Red} {2,718281}}693\cdots </math>  
+
−
|-
+
−
| align=left| <math> 100\,000\,000 </math> ||align=left| <math> {\color{Red} {2,7182818}}15\cdots </math>  
+
−
|-
+
−
| align=left| <math> 1000\,000\,000 </math> ||align=left| <math> {\color{Red} {2,71828182}}7\cdots </math>  
+
−
|-
+
−
| align=left| <math> 10\,000\,000\,000 </math> ||align=left| <math> {\color{Red} {2,718281828}}\cdots </math>
+
−
|-
+
−
! <math> \infty </math> || <math> {\color{Red} {{\rm Eulers\;tal\;} e}} </math>
+
 
|}
 
|}
−
De korrekta siffrorna är rödmarkerade och visar hur uttrycket sakta men säkert konvergerar mot det värde du fick fram i räknaren när du slog in <big><math> e^{\,1} \, </math></big>. Så i fortsättningen när vi räknar med talet <big><math> e \,</math></big> nöjer vi oss med följande närmevärde med nio decimaler:
+
</small></div>
  
−
:::::::::::<big><math> e \; = \; 2,718281828\cdots </math></big>
+
De korrekta siffrorna är rödmarkerade och visar hur uttrycket sakta men säkert konvergerar mot det värde man får i räknaren när man slår in <big><math> e^{\,1} \, </math></big>.
 +
 
 +
<b><span style="color:red">Eulers formel</span></b> ger oss en algoritm för att med hjälp av heltalen <math> \, n \, </math> närma oss det irrationella talet <big><math> \, e \, </math></big> (tabellen ovan).
 +
 
 +
Så i fortsättningen när vi räknar med talet <big><math> e \,</math></big> nöjer vi oss med följande närmevärde med nio decimaler:
 +
 
 +
:::::::::<big><math> e \; = \; {\color{Red} {2,718281828\ldots}} </math></big>
 
</big></div>
 
</big></div>
  
 +
 +
== <b><span style="color:#931136">Exponentialfunktionen med basen <big><math> e \,</math></big></span></b> ==
  
 
<big>
 
<big>
−
Repetera ina kunskaper från Matte 2 om [[Exponentialfunktioner och logaritmer|<strong><span style="color:blue">exponentialfunktioner och logaritmer</span></strong>]] samt [[Logaritmlagarna|<strong><span style="color:blue">logaritmlagarna</span></strong>]].
+
Tar man talet <big><math> {\color{Red} e} </math></big> som bas och bildar potensen <big><math> {\color{Red} {e{\,^x}}} </math></big> får man den s.k. <b><span style="color:red">exponentialfunktionen</span></b> <big><math> {\color{Red} {y = e{\,^x}}} </math></big> <b><span style="color:red">med basen</span></b> <big><math> {\color{Red} e} \, </math></big> som har stor betydelse inom naturvetenskap, teknik och ekonomi:
  
−
I repetitionen har vi pratat om exponentialfunktion'''er''', dvs i pluralis, därför att vi där inte hade specificerat basen. Det beror på vilken bas man väljer, t.ex. <math> y = 2\,^x </math> eller <math> y = 3\,^x,\;\cdots </math> . I detta avsnitt väljer vi Eulers tal <math> e \,</math> som bas och tittar på <math> \, y = e\,^x </math>.
+
 
 +
<div class="border-div"> <big><big><math> y \; = \; e\,^x </math></big></big> </div> &nbsp;&nbsp;&nbsp;&nbsp;&nbsp; med grafen:  &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: exp.jpg]]
 +
 
 +
::::::::::::::<b><span style="color:red">Exponentialfunktionen med basen <big><math> \; {\color{Red} e} </math></big></span></b>
 
</big>
 
</big>
  
 +
<div class="ovnC">
 +
==== <b><span style="color:#931136">Egenskaper</span></b> ====
 +
 +
<div class="exempel">
 +
# Exponentialfunktionen är alltid <b>positiv</b><span style="color:black">:</span> <math> \, e\,^x \, > \, 0 \, </math> för alla <math> \, x </math>. Den blir aldrig <math> 0\, </math> eller negativ. Definitionsmängden<span style="color:black">:</span> <b> alla </b> <math> x </math>.
 +
# <math> e\,^0 = 1 </math> vilket följer av potenslagen om nollte potens.
 +
# För negativa <math> \, x \, </math> är <math> \, e\,^x < 1 </math>. För positiva <math> \, x \, </math> är <math> \, e\,^x > 1 </math> och växer allt starkare ju större <math> \, x \, </math> blir.
 +
# Exponentialfunktionen växer starkast bland alla (hittills för oss kända) matematiska funktioner.
 +
</div>
 +
 +
<b><span style="color:#931136">Exponentiell tillväxt</span></b> modelleras med exponentialfunktioner av typ <math> \, y = C \cdot e\,^{k \, x} \, </math> med <math> \, k \, {\color{Red} >} \, 0 </math>.
 +
 +
<b><span style="color:#931136">Exponentiell minskning</span></b> modelleras med exponentialfunktioner av typ <math> \, y = C \cdot e\,^{k \, x} \, </math> med <math> \, k \, {\color{Red} <} \, 0 </math>.
 +
</div>
  
−
== <b><span style="color:#931136">Exponentialfunktionen med basen <big><math> e \,</math></big></span></b> ==
 
  
 
<big>
 
<big>
−
<div class="border-div"> <big><big><math> y \; = \; e\,^x </math></big></big> </div> &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; med grafen:  &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image: exp.jpg]]
+
Exponentiell tillväxt (eller minskning) förekommer både i naturvetenskapliga och ekonomiska tillämpningar. Den har en starkare takt än t.ex. potensfunktionen <math> \, y = x^2 \, </math> som har kvadratisk tillväxt. Testa gärna genom att rita grafen till <math> \, y = x^2 \, </math> och <math> \, y = e\,^x \, </math> i ett och samma koordinatsystem och jämföra kurvornas branthet.
  
−
::::::::::::<b><strong><span style="color:red">Exponentialfunktionen med basen <big><math> \; {\color{Red} {e = 2,718281828 \ldots}} </math></big></span></strong></b>
+
I repetitionen [[Repetition: Exponentialfunktioner|<b><span style="color:blue">Exponentialfunktioner</span></b>]] hade vi pratat om exponentialfunktion'''er''' (i pluralis) därför att vi där inte hade valt en speciell bas. Vilken exponentialfunktion man menar beror på vilken bas man väljer, t.ex. <math> y = 2\,^x </math> eller <math> y = 3\,^x,\;\cdots </math>.
  
 +
När man däremot pratar om '''den''' exponentialfunktionen (i singularis) utan att nämna basen menar man alltid exponentialfunktionen med basen <big><math> \, e\,</math></big> <math>-</math> som en slags prototyp för alla exponentialfunktioner.
 +
</big>
  
−
När matematiker pratar om '''den''' exponentialfunktionen (i singularis) utan att specificiera basen menar de alltid denna exponentialfunktion med basen <math>e\,</math> <math>-</math> som en slags prototyp för alla exponentialfunktioner. Även vi kommer att använda oss av denna konvention. Att basen <math>e\,</math> har en sådan särställning beror på dess betydelse inom den gren av matematiken som vi börjar att studera i nästa kapitel Derivata.
 
  
 +
== <b><span style="color:#931136">Den naturliga logaritmen</span></b> ==
 +
<div class="ovnC">
 +
<big><b><span style="color:#931136">Experiment 2</span></b></big> <math> \qquad </math> Ta fram din miniräknare och gör så här:
  
 +
# Tryck på funktionsknappen <math> \, \boxed{e^{\,x}} </math> och mata in<span style="color:black"></span> <big><math> \quad \color{Red}{\boxed{2}} \quad </math></big> och stäng parentesen.
 +
# Tryck på ENTER när det står <big><math> \, e </math></big> <span style="color:black">''^''</span> <math>(2) \; </math> i displayen. Låt resultatet <math> \, e^{\,2} \, </math> (något decimaltal) stå i displayen.
 +
# Tryck på funktionsknappen<span style="color:black"></span> <math> \, \boxed{\rm{LN}} \, </math>.
 +
# Mata in ANS som står för ANSwer och lagrar räknarens sist beräknade värde, i vårt fall <math> \, e^{\,2} </math>.
 +
# Stäng parentesen och tryck på ENTER: Du får tillbaka <big><math> \quad \color{Red}{\boxed{2}} \quad </math></big> som du hade matat in i början.
  
−
<div class="ovnE">
+
Du har beräknat <math> \, \ln\,(e^{\,2}) </math> som ger <math> \, 2 \, </math>, dvs: <big><math> \qquad\quad\;\;\; \ln\,(e^{\,2}) \, = \, 2 </math></big>
−
=== <b><span style="color:#931136">Några egenskaper hos exponentialfunktionen</span></b> ===
+
  
−
<div class="exempel">
+
Genomför ett liknande experiment som visar: <big><math> \qquad\qquad e^{\,\ln 2} \, = \, 2 \, </math></big>
−
# Exponentialfunktionen är definierad <b> för alla </b> <math> x\, </math> och är alltid positiv, dvs <math> e\,^x \; > \; 0 </math> <b> för alla </b> <math> x\, </math>. Den blir aldrig <math> 0\, </math> eller negativ.
+
−
# <math> e\,^0 = 1 </math> vilket är förstås en konsekvens av potenslagarna.
+
−
# För lagom små <math> x\, </math> har exponentialfunktionen väldigt små värden och för lagom stora <math> x\, </math> har den väldigt stora värden.
+
−
# Exponentialfunktionen växer allt brantare ju större <math> x\, </math> är.
+
 
</div>
 
</div>
  
−
Nu ersätter vi <math> \, 4 \, </math> med <math> \, 0 \, </math>:
+
<big>I räknaren står <math> \boxed{\rm{LN}} </math> för <big>L</big><b><span style="color:red">ogaritmus</span></b> <big>N</big><b><span style="color:red">aturalis</span></b>, den naturliga logaritmen, medan <math> \boxed{\rm{LOG}} </math> står för [[Repetition: 10-logaritmer|<b><span style="color:blue"><math> \, 10</math>-logaritmer</span></b>]].
 +
 
 +
När man skriver står <b><span style="color:red"><math>\ln</math></span></b> för <b><span style="color:red">l</span>ogaritmus</b> <b><span style="color:red">n</span>aturalis</b> och är symbolen för den naturliga logaritmen.
 +
 
 +
Talet <big><math> \, e \, </math></big> bildar basen till <b><span style="color:red"><math>\ln</math></span></b>.
 +
</big>
 +
 
 +
<div class="ovnE">
 +
<big>
 +
<b><span style="color:#931136">Exempel:</span></b>
 +
 
 +
<math>\ln 3 \, </math> = <b><span style="color:red">Exponent</span></b> som basen <math> \, e \, </math> ska upphöjas till, för att ge <math> \, 3 \, </math><span style="color:black">:</span>
 +
 
 +
<math> \quad e\,^{\color{Red} {1,09861\ldots}} \; = \; 3 \qquad \Leftrightarrow \qquad {\color{Red} {1,09861\ldots}} \; = \; \ln\,3 </math>
 +
 
 +
----
 +
 
 +
I räknaren<span style="color:black">:</span> <small><math> \qquad\qquad\quad \boxed{\text{LN}}</math></small> <math>(3) \; = \; {\color{Red} {1,09861\ldots}} </math>
 +
</big></div>
 +
 
 +
<big>
 +
Generellt:
 +
 
 +
<div class="border-divblue">
 +
<b><span style="color:#931136">Definition:</span></b>
 +
 
 +
<math>\ln a \, </math> = <b><span style="color:red">Exponenten</span></b> <big><math> \color{Red} x </math></big> som basen <big><math> \, e \, </math></big> ska upphöjas till, för att ge <math> \, a \, </math><span style="color:black">:</span>
 +
 
 +
<math> \qquad\qquad\quad </math>  <big><math> e^{\color{Red} x} = a \qquad \Leftrightarrow \qquad {\color{Red} x} = \ln\,a </math></big>
 
</div>
 
</div>
  
−
De sista två egenskaperna brukar man ofta uttrycka så att man säger att tillväxten hos en process är <strong><span style="color:red">exponentiell</span></strong>. Exponentiell tillväxt förekommer både i naturvetenskapliga och ekonomiska tillämpningar. Den har en starkare takt än alla andra tillväxttyper som t.ex. kan beskrivas med potensfunktioner av typ <math> x^2\, </math> (kvadratisk) eller <math> x^3\, </math> (kubisk) osv. För att övertyga dig om detta kan du rita graferna till potensfunktionerna <math> y = x^n\,</math> för n = 1, 2, 3, ... och exponentialfunktionen <math> y = e\,^x </math> i ett och samma koordinatsystem och jämföra kurvornas branthet.
 
  
 +
Exponentialfunktionen <math> \, y = e\,^x \, </math> ger upphov till den <b><span style="color:red">naturliga logaritmfunktionen</span></b> <math> \, {\color{Red} {y = \ln x}} \, </math>:
  
−
== Den naturliga logaritmen ==
+
<div class="border-div"> <big><big><math> y \; = \; \ln\, x </math></big></big> </div> &nbsp;&nbsp;&nbsp;&nbsp;&nbsp; med grafen:  &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image: ln.jpg]]
  
−
Precis som alla exponentialfunktioner som har sina inversa logaritmfunktioner <math>-</math> bland dem <math> y = 10\,^x</math> med inversen <math> y = \lg\,x </math>  <math>-</math> har även exponentialfunktionen <math> y = e\,^x </math> med basen <math> e\, </math> sin inversa logaritmfunktion till basen <math> e\, </math> dvs <math> y = \log_e\,x </math>. Logaritmen till denna bas kallas <strong><span style="color:red">den naturliga logaritmen</span></strong>. Och precis som 10-logaritmen har förkortningen <math> \lg\, </math>, har den naturliga logaritmen förkortningen <big><math> \ln\, </math></big> eller <big> LN </big> som står för <strong><span style="color:red">logaritmus naturalis</span></strong>.
+
:::::::::::::::<b><span style="color:red">Den naturliga logaritmfunktionen</span></b>
 +
</big>
  
 +
<div class="ovnC">
 +
==== <b><span style="color:#931136">Egenskaper</span></b> ====
  
−
<div class="border-div">
+
<div class="exempel">
−
<big><math> y \; = \; \ln x \qquad {\rm logaritmen\;med\;basen} \quad  e = 2,718281828\cdots </math></big>
+
# Logaritmen är definierad endast för <b>positiva <math> \, x\, </math></b>. Definitionsmängden<span style="color:black">:</span> <math> \, x > 0 </math>.
 +
# <math> \ln\,1 = 0 \, </math> vilket är logaritmformen till <math> \, e\,^0 = 1 </math>, se egenskap 2 hos exponentialfunktionen.
 +
# För <math> x < 1\, </math> är logaritmen negativ och för <math> x > 1\, </math> är den positiv.
 +
# Logaritmen växer allt svagare ju större <math> \, x\, </math> är.
 
</div>
 
</div>
  
 +
&nbsp; <b><span style="color:red">OBS! &nbsp; Logaritmen är för <math> \, x=0 \, </math> inte alls och för <math> \, x<0 \, </math> inte definierad inom de reella talen.</span></b>
 +
</div>
  
−
Båda logaritmerna <math> \lg\, </math> och <math> \ln\, </math> <math>-</math> och endast dessa två <math>-</math> är inprogrammerade i alla (tekniska) kalkylatorer. Däremot har de i räknaren knapparna <big> LOG </big> som står för 10-logaritmen och <big> LN </big> som står för den naturliga logaritmen dvs logaritmen med basen <math> e\, </math>.
 
  
 +
<big>För <math> \, x < 0 \, </math> har <math> \, y \, = \, \ln x \, </math> komplexa värden.
  
−
== Inversegenskapen ==
+
Här behandlas den naturliga logaritmen endast inom de reella talen.</big>
  
−
Ta fram din miniräknare och beräkna:
 
  
−
::::::::::::<big><math> e^{\,2} </math></big>
+
== <b><span style="color:#931136">Inversegenskapen</span></b> ==
  
−
Om du inte vet hur det går tryck på den gröna knappen 2nd och sedan på LN vilket ger exponentialfunktionen <math> e^{\,x} </math>. När du ser <math> e \, </math> <big>''^''</big> <math> ( \, </math> i displayen, mata in <math> 2 \, </math>, stäng parentesen och tryck på ENTER. Så får du något decimaltal som är <math> e^{\,2} </math>. Låt resultatet stå i displayen.
+
<big>
 +
<b><span style="color:#931136">Experiment 2</span></b> visar ett exempel på att <math> \, \boxed{\rm{LN}} \, </math> är den inversa operationen till <math> \, \boxed{e\,^x} \, </math>.
  
−
Fortsätt med att beräkna <math> \ln\,(e^{\,2}) </math>, så här: Tryck på knappen LN, på den gröna knappen 2nd och sedan på knappen (-) vilket ger ANS som står för ANSwer och lagrar räknarens sist beräknade värde, i vårt fall decimaltalet <math> e^{\,2} </math>. Stäng parentesen och tryck på ENTER så får du tillbaka din <math> \, 2</math>:a som du hade matat in i exponentialfunktionen <math> e^{\,x} </math>. Du har beräknat <math> \ln\,(e^{\,2}) </math> som ger <math> \, 2 </math>:
+
Generellt:
 +
<div class="border-divblue">
 +
Den naturliga logaritmen <math> \, y \, = \, \ln\,x \, </math> är den <b><span style="color:red">inversa</span></b> (motsatta) funktionen till exponentialfunktionen <math> \, y \, = \, e\,^x \, </math><span style="color:black">:</span>
  
−
::::::::::::<big><math> \ln\,(e^{\,2}) \, = \, 2 </math></big>
+
:::<math> \ln\,(e^{\,x}) \, = \, x \qquad {\rm och\; } \qquad e^{\,\ln\,x} \, = \, x \qquad\quad {\rm I\;ord:\quad } e^{\,x} {\rm \;och\; } \ln\,x \;{\rm {\color {Red} {tar\;ut\;varandra}}.} </math>
 +
</div></big>
  
−
Med detta experiment <math>-</math> du kan gärna upprepa det med andra tal <math>-</math> har du exemplifierat den allmänna <strong><span style="color:red">inversegenskapen</span></strong> för exponential- och logaritmfunkhionen. De är <strong><span style="color:red">inversa</span></strong> till varandra (omvända operationer) och tar därför ut varandra. Matematiskt uttryckt innebär detta:
 
  
 +
:::::::::::[[Image: InvEgenskap_Farg.jpg]]
  
−
<div class="border-div">
 
−
<big><math> \ln\,(e^{\,x}) \, = \, x \qquad {\rm och\; } \qquad e^{\,\ln\,x} \, = \, x \qquad\quad {\rm dvs:\; } e^{\,x} {\rm \;och\; } \ln\,x \;{\rm {\color {Red} {tar\;ut\;varandra}}.} </math></big>
 
−
</div>
 
  
 +
<big>
 +
Inversegenskapen gäller oberoende av operationernas ordning: Vare sig du tar först <math> e^{\,x} </math> och sedan <math> \ln\,x </math> eller tvärt om, resultatet blir alltid <math> \,x </math>.
  
−
Inversegenskapen gäller alltså oberoende av operationernas ordning: Vare sig du tar först <math> e^{\,x} </math> och sedan <math> \ln\,x </math> eller tvärt om, resultatet blir alltid <math> \,x </math>. Dvs man återvänder till det värde <math> \,x </math> man hade börjat att använda någon av dessa operationer på. Förutsättningen är förstås att man tillämpar <math> e^{\,x} </math> och <math> \ln\,x </math> <b>direkt</b> efter varandra.
+
Dvs man återvänder till det värde <math> \,x </math> man hade börjat att använda någon av dessa operationer på. Förutsättningen är förstås att man utför <math> e^{\,x} </math> och <math> \ln\,x </math> direkt efter varandra.
  
−
Både <math> \ln\,(e^{\,x}) </math> och <math> e^{\,\ln\,x} </math> är exempel på s.k. <strong><span style="color:red">sammansatta funktioner</span></strong>. För sådana funktioner gäller regeln: Sammansatta funktioner exekveras (beräknas) inifrån. Ditt eget experiment var ett exempel på detta: Du beräknade först <math> e^{\,2} </math> och sedan <math> \ln\,(e^{\,2}) </math>.
+
Både <math> \ln\,(e^{\,x}) </math> och <math> e^{\,\ln\,x} </math> är exempel på s.k. <b><span style="color:red">sammansatta funktioner</span></b>. För sådana funktioner gäller regeln:
  
−
Så här kan man tänka sig att inversegenskapen för exponential- och logaritmfunkhionen fungerar oberoende av operationernas ordning:
+
Sammansatta funktioner beräknas <b><span style="color:red">inifrån</span></b>: [[1.4_Talet_e_och_den_naturliga_logaritmen#Experiment_2|<b><span style="color:blue">Experiment 2</span></b>]] var ett exempel på detta. För att få <math> \, \ln\,(e^{\,2}) \, </math>, beräknades först <math> \, e^{\,2} </math> och sedan <math> \, \ln\,(e^{\,2}) </math>.
 +
</big>
  
−
::[[Image: InvEgenskap_Farg.jpg]]
 
  
 +
== <b><span style="color:#931136">Exponentialekvationen av typ <math> \; e\,^x \, = \, b </math></span></b> ==
  
−
== Ekvationen &nbsp; <math> e\,^x \, = \, b </math> ==
+
<big>
−
[[Image: Naturliga_logaritmen_40.jpg]]
+
Precis som [[Repetition:_10-logaritmer#Exponentialekvationer_av_typ_.5C.28_.5C.3B_10.5C.2C.5Ex_.5C.2C_.3D_.5C.2C_b_.5C.29|<b><span style="color:blue">exponentialekvationen <math> \, 10\,^x \, = \, b \; </math></span></b>]] löstes med den inversa operationen till <math> \, 10\,^x </math>, nämligen <math> \, 10</math>-logaritmen, löses ekvationen ovan med den inversa operationen till <math> \, e\,^x </math>, nämligen den naturliga logaritmen.
−
== Egenskaper hos <big><math> y = \ln x </math></big> ==
+
</big>
  
  
 +
<div class="ovnE">
 +
<big><b><span style="color:#931136">Exempel</span></b></big>
  
−
::[[Image: Den naturliga logaritmen.jpg]]
+
<div class="exempel">
 +
<math>\begin{array}{rcll}            e^{\,x} & = & 68                &  {\rm Logaritmera\;båda\;leden\;med\;\ln} \\
 +
{\color{Red} {\ln}}\,({\color{Red} e}^{\,x}) & = & \ln\,68          &  {\rm Använd\;inversegenskapen\;på\;VL}  \\
 +
                                          x & = & \ln\,68          &                                            \\
 +
                                          x & = & 4,219507705\ldots &                                            \\
 +
    {\rm Kontroll:\qquad} e^{\,4,219507705} & = & 68                & 
 +
        \end{array}</math>
 +
</div></div>
  
  
−
Några egenskaper hos den naturliga logaritmfunktionen <math> y = \ln\,x </math> som man kan avläsa från grafen, är:
 
  
−
# Logaritmen är definierad endast för <b>positiva <math> x\, </math></b>. Den är inte definierad för <math> x\leq 0\, </math>.
 
−
# <math> \ln\,1 = 0 </math> vilket är logaritmformen till den nollte potensen <math> e\,^0 = 1 </math>.
 
−
# För <math> x < 1\, </math> är logaritmen negativ och för <math> x > 1\, </math> är den positiv.
 
−
# Logaritmen växer allt svagare ju större <math> x\, </math> är.
 
  
−
Dessa egenskaper gäller även för logaritmer till andra baser.
 
  
  
Rad 196: Rad 267:
  
  
−
[[Matte:Copyrights|Copyright]] © 2011-2015 Taifun Alishenas. All Rights Reserved.
+
[[Matte:Copyrights|Copyright]] © 2019 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved.

Nuvarande version från 6 maj 2019 kl. 18.04

        <<  Förra avsnitt          Rep.: 10-logaritmer          Genomgång          Övningar          Nästa avsnitt  >>      
       Rep.: Exponentialfunktioner          Rep.: Logaritmlagarna          Genomgång          Övningar          Nästa avsnitt  >>      


Talet  \( e \,\)

Experiment 1 \( \qquad \) Ta fram din miniräknare och gör så här:

  1. Leta efter funktionsknappen (ev. med hjälp av 2nd-knappen) \( \quad \boxed{e^{\,x}} \;\; \)
  2. Tryck på den, mata in \( \, 1 \, \) och stäng parentesen.
  3. Tryck på ENTER när det står \( \, e \) ^ \((1) \; \) i räknarens display.

Du har beräknat \( \; e{\,^1} \; \) eller talet \( \, \color{blue} e \,\), dvs \( \qquad 2,718281828\ldots \quad \),

en av matematikens mest kända konstanter, även kallad Eulers tal.


Talet \( \, \color{blue} e \, \) är kallat efter den tysk-schweiziske matematikern Leonard Euler som på 1700-talet definierade detta märkliga tal.

Märkligt, därför att \( \, e \, \) inte är ett "vanligt" tal som heltal eller bråk. Det är inte ett rationellt tal, se olika typer av tal.

Talet \( \, e \, \) är ett irrationellt tal, precis som talen \( \pi,\, \sqrt{2},\, \sqrt{3},\,\ldots \, \), som inte kan skrivas i bråkform.

Irrationella tal är decimaltal som har en icke-periodisk decimalutveckling dvs oändligt många decimaler utan något upprepande mönster (period).

Här kan man beskåda de första 5 miljoner decimaler av talet \( \, e \, \). Leta gärna efter ett upprepande mönster! Du kommer inte att hitta något.

  OBS! \( \quad e \; \) är ingen variabel utan en s.k. namngiven konstant som har värdet \( \, 2,718281828\ldots \, \).

Talet \( \, e \, \) förekommer bl.a. i en formel som enligt många är en av matematikens vackraste, nämligen sambandet mellan heltalet \( 1\, \), de irrationella talen \( e,\;\pi \) och den imaginära enheten \( \, i = \sqrt{-1} \), där även \( \pi \) och \( \, i \, \) är namngivna konstanter:

\( e^{\,2\,\pi\,i} \) \( = 1 \)

Ingen fara, vi har inte för avsikt att närmare gå in på denna formel. Vi nämner den bara för att illustrera betydelsen av talet \( \, e \, \) inom den matematiska analysen, den delen av matematiken som behandlar gränsvärden, derivator, integraler och differentialekvationer.


Hur kom(mer) talet \( e \,\) till?

Eulers formel kan användas för att numeriskt få fram några decimaler av talet \( e \,\):

\( \left(1 + {1 \over n}\right)^n \to \; e \) \( \quad {\rm när} \quad n \to \infty \)

Dvs: Uttrycket ovan går mot \( e \,\) när \( n\, \) går mot oändligheten (\( \infty \)) eller:

Uttrycket närmar sig allt mer \( \, e \,\) ju större \( \, n\, \) blir. Tabellen tar några steg i denna process:

\( n \) \( 1\,000 \) \( 1000\,000 \) \( 1000\,000\,000 \) \( 10\,000\,000\,000 \) \( \to \infty \)
\( \left(1 + {1 \over n}\right)^n \) \( {\color{Red} {2,71}}6923932\ldots \) \( {\color{Red} {2,71828}}0469\ldots \) \( {\color{Red} {2,71828182}}7\ldots \) \( {\color{Red} {2,718281828\ldots}} \) \( \quad \to \; {\color{Red} {{\rm Eulers\;tal\;} e}} \quad \)

De korrekta siffrorna är rödmarkerade och visar hur uttrycket sakta men säkert konvergerar mot det värde man får i räknaren när man slår in \( e^{\,1} \, \).

Eulers formel ger oss en algoritm för att med hjälp av heltalen \( \, n \, \) närma oss det irrationella talet \( \, e \, \) (tabellen ovan).

Så i fortsättningen när vi räknar med talet \( e \,\) nöjer vi oss med följande närmevärde med nio decimaler:

\( e \; = \; {\color{Red} {2,718281828\ldots}} \)


Exponentialfunktionen med basen \( e \,\)

Tar man talet \( {\color{Red} e} \) som bas och bildar potensen \( {\color{Red} {e{\,^x}}} \) får man den s.k. exponentialfunktionen \( {\color{Red} {y = e{\,^x}}} \) med basen \( {\color{Red} e} \, \) som har stor betydelse inom naturvetenskap, teknik och ekonomi:


\( y \; = \; e\,^x \)
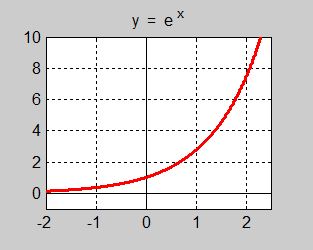
      med grafen:       Exp.jpg
Exponentialfunktionen med basen \( \; {\color{Red} e} \)

Egenskaper

  1. Exponentialfunktionen är alltid positiv: \( \, e\,^x \, > \, 0 \, \) för alla \( \, x \). Den blir aldrig \( 0\, \) eller negativ. Definitionsmängden: alla \( x \).
  2. \( e\,^0 = 1 \) vilket följer av potenslagen om nollte potens.
  3. För negativa \( \, x \, \) är \( \, e\,^x < 1 \). För positiva \( \, x \, \) är \( \, e\,^x > 1 \) och växer allt starkare ju större \( \, x \, \) blir.
  4. Exponentialfunktionen växer starkast bland alla (hittills för oss kända) matematiska funktioner.

Exponentiell tillväxt modelleras med exponentialfunktioner av typ \( \, y = C \cdot e\,^{k \, x} \, \) med \( \, k \, {\color{Red} >} \, 0 \).

Exponentiell minskning modelleras med exponentialfunktioner av typ \( \, y = C \cdot e\,^{k \, x} \, \) med \( \, k \, {\color{Red} <} \, 0 \).


Exponentiell tillväxt (eller minskning) förekommer både i naturvetenskapliga och ekonomiska tillämpningar. Den har en starkare takt än t.ex. potensfunktionen \( \, y = x^2 \, \) som har kvadratisk tillväxt. Testa gärna genom att rita grafen till \( \, y = x^2 \, \) och \( \, y = e\,^x \, \) i ett och samma koordinatsystem och jämföra kurvornas branthet.

I repetitionen Exponentialfunktioner hade vi pratat om exponentialfunktioner (i pluralis) därför att vi där inte hade valt en speciell bas. Vilken exponentialfunktion man menar beror på vilken bas man väljer, t.ex. \( y = 2\,^x \) eller \( y = 3\,^x,\;\cdots \).

När man däremot pratar om den exponentialfunktionen (i singularis) utan att nämna basen menar man alltid exponentialfunktionen med basen \( \, e\,\) \(-\) som en slags prototyp för alla exponentialfunktioner.


Den naturliga logaritmen

Experiment 2 \( \qquad \) Ta fram din miniräknare och gör så här:

  1. Tryck på funktionsknappen \( \, \boxed{e^{\,x}} \) och mata in \( \quad \color{Red}{\boxed{2}} \quad \) och stäng parentesen.
  2. Tryck på ENTER när det står \( \, e \) ^ \((2) \; \) i displayen. Låt resultatet \( \, e^{\,2} \, \) (något decimaltal) stå i displayen.
  3. Tryck på funktionsknappen \( \, \boxed{\rm{LN}} \, \).
  4. Mata in ANS som står för ANSwer och lagrar räknarens sist beräknade värde, i vårt fall \( \, e^{\,2} \).
  5. Stäng parentesen och tryck på ENTER: Du får tillbaka \( \quad \color{Red}{\boxed{2}} \quad \) som du hade matat in i början.

Du har beräknat \( \, \ln\,(e^{\,2}) \) som ger \( \, 2 \, \), dvs: \( \qquad\quad\;\;\; \ln\,(e^{\,2}) \, = \, 2 \)

Genomför ett liknande experiment som visar: \( \qquad\qquad e^{\,\ln 2} \, = \, 2 \, \)

I räknaren står \( \boxed{\rm{LN}} \) för Logaritmus Naturalis, den naturliga logaritmen, medan \( \boxed{\rm{LOG}} \) står för \( \, 10\)-logaritmer.

När man skriver står \(\ln\) för logaritmus naturalis och är symbolen för den naturliga logaritmen.

Talet \( \, e \, \) bildar basen till \(\ln\).

Exempel:

\(\ln 3 \, \) = Exponent som basen \( \, e \, \) ska upphöjas till, för att ge \( \, 3 \, \):

\( \quad e\,^{\color{Red} {1,09861\ldots}} \; = \; 3 \qquad \Leftrightarrow \qquad {\color{Red} {1,09861\ldots}} \; = \; \ln\,3 \)

I räknaren: \( \qquad\qquad\quad \boxed{\text{LN}}\) \((3) \; = \; {\color{Red} {1,09861\ldots}} \)

Generellt:

Definition:

\(\ln a \, \) = Exponenten \( \color{Red} x \) som basen \( \, e \, \) ska upphöjas till, för att ge \( \, a \, \):

\( \qquad\qquad\quad \) \( e^{\color{Red} x} = a \qquad \Leftrightarrow \qquad {\color{Red} x} = \ln\,a \)


Exponentialfunktionen \( \, y = e\,^x \, \) ger upphov till den naturliga logaritmfunktionen \( \, {\color{Red} {y = \ln x}} \, \):

\( y \; = \; \ln\, x \)
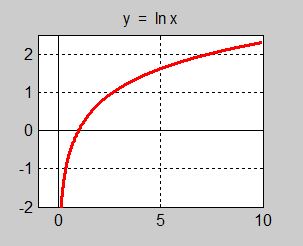
      med grafen:        Ln.jpg
Den naturliga logaritmfunktionen

Egenskaper

  1. Logaritmen är definierad endast för positiva \( \, x\, \). Definitionsmängden: \( \, x > 0 \).
  2. \( \ln\,1 = 0 \, \) vilket är logaritmformen till \( \, e\,^0 = 1 \), se egenskap 2 hos exponentialfunktionen.
  3. För \( x < 1\, \) är logaritmen negativ och för \( x > 1\, \) är den positiv.
  4. Logaritmen växer allt svagare ju större \( \, x\, \) är.

  OBS!   Logaritmen är för \( \, x=0 \, \) inte alls och för \( \, x<0 \, \) inte definierad inom de reella talen.


För \( \, x < 0 \, \) har \( \, y \, = \, \ln x \, \) komplexa värden.

Här behandlas den naturliga logaritmen endast inom de reella talen.


Inversegenskapen

Experiment 2 visar ett exempel på att \( \, \boxed{\rm{LN}} \, \) är den inversa operationen till \( \, \boxed{e\,^x} \, \).

Generellt:

Den naturliga logaritmen \( \, y \, = \, \ln\,x \, \) är den inversa (motsatta) funktionen till exponentialfunktionen \( \, y \, = \, e\,^x \, \):

\[ \ln\,(e^{\,x}) \, = \, x \qquad {\rm och\; } \qquad e^{\,\ln\,x} \, = \, x \qquad\quad {\rm I\;ord:\quad } e^{\,x} {\rm \;och\; } \ln\,x \;{\rm {\color {Red} {tar\;ut\;varandra}}.} \]


InvEgenskap Farg.jpg


Inversegenskapen gäller oberoende av operationernas ordning: Vare sig du tar först \( e^{\,x} \) och sedan \( \ln\,x \) eller tvärt om, resultatet blir alltid \( \,x \).

Dvs man återvänder till det värde \( \,x \) man hade börjat att använda någon av dessa operationer på. Förutsättningen är förstås att man utför \( e^{\,x} \) och \( \ln\,x \) direkt efter varandra.

Både \( \ln\,(e^{\,x}) \) och \( e^{\,\ln\,x} \) är exempel på s.k. sammansatta funktioner. För sådana funktioner gäller regeln:

Sammansatta funktioner beräknas inifrån: Experiment 2 var ett exempel på detta. För att få \( \, \ln\,(e^{\,2}) \, \), beräknades först \( \, e^{\,2} \) och sedan \( \, \ln\,(e^{\,2}) \).


Exponentialekvationen av typ \( \; e\,^x \, = \, b \)

Precis som exponentialekvationen \( \, 10\,^x \, = \, b \; \) löstes med den inversa operationen till \( \, 10\,^x \), nämligen \( \, 10\)-logaritmen, löses ekvationen ovan med den inversa operationen till \( \, e\,^x \), nämligen den naturliga logaritmen.


Exempel

\(\begin{array}{rcll} e^{\,x} & = & 68 & {\rm Logaritmera\;båda\;leden\;med\;\ln} \\ {\color{Red} {\ln}}\,({\color{Red} e}^{\,x}) & = & \ln\,68 & {\rm Använd\;inversegenskapen\;på\;VL} \\ x & = & \ln\,68 & \\ x & = & 4,219507705\ldots & \\ {\rm Kontroll:\qquad} e^{\,4,219507705} & = & 68 & \end{array}\)




Internetlänkar

https://www.youtube.com/watch?v=X-z0aw_q7yM

http://www.youtube.com/watch?v=Z3xsdOvjl4E

http://www.youtube.com/watch?v=_FZJiyqIrG4&feature=related

http://www.youtube.com/watch?v=7RAWXVoyls4





Copyright © 2019 TechPages AB. All Rights Reserved.

Hämtad från "https://matte3c.mathonline.se/index.php?title=1.4_Talet_e_och_den_naturliga_logaritmen&oldid=36576"