Skillnad mellan versioner av "2.6 Derivatan av exponentialfunktioner"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (618 mellanliggande versioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
| + | __NOTOC__ | ||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| − | {{ | + | {{Not selected tab|[[2.5 Deriveringsregler| << Förra avsnitt]]}} |
| − | {{Not selected tab|[[2. | + | {{Selected tab|[[2.6 Derivatan av exponentialfunktioner|Genomgång]]}} |
| + | {{Not selected tab|[[2.6 Övningar till Derivatan av exponentialfunktioner|Övningar]]}} | ||
| + | {{Not selected tab|[[2.7 Numerisk derivering|Nästa avsnitt >> ]]}} | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| − | + | <!-- [[Media: Lektion 19 Derivat Expfkt Ruta.pdf|<b><span style="color:blue">Lektion 19 Derivatan av exponentialfunktioner</span></b>]] --> | |
| − | + | ||
| − | + | ||
| − | + | <big> | |
| + | Målet i detta avsnitt är att ställa upp deriveringsregeln för den allmänna exponentialfunktionen <math> \, y = a\,^x \, </math> med en godtycklig bas <math> a > 0 </math>. | ||
| − | + | Detta gör vi genom att först härleda derivatan av exponentialfunktionen <math> \, y = e\,^x \, </math> med basen <math> \, e = </math> Eulers tal | |
| − | + | och sedan gå över till godtycklig bas <math> \,a </math>. Rpeptera gärna [[1.4 Talet e och den naturliga logaritmen|<b><span style="color:blue">Talet e och den naturliga logaritmen</span></b>]] från kap 1 Algebra & funktioner. | |
| − | |||
| − | + | === <b><span style="color:#931136">Deriveringsregeln för <math> y \, = \, e\,^x </math></span></b> === | |
| − | + | <div class="border-divblue"> | |
| + | Derivatan av exponentialfunktionen med basen <math> \, e \, </math> är funktionen själv: | ||
| − | + | ::::<math> \begin{array}{llcl} {\rm Om} & y & = & e\,^x \;\; {\rm där} \;\; e = {\rm Eulers\;tal} \\ | |
| + | {\rm då} & y\,' & = & e\,^x | ||
| + | \end{array}</math> | ||
| + | </div> | ||
| − | [[ | + | '''OBS!''' Förväxla denna regel inte med [[2.5_Deriveringsregler#Derivatan_av_en_potens|<b><span style="color:blue">Regeln om derivatan av en potens</span></b>]], därför att<span style="color:black">:</span> |
| − | + | <math> y \, = \, e\,^x \, </math> är ingen potens- utan en exponentialfunktion. <math> \, x \, </math> förekommer i exponenten, inte i basen. | |
| − | = | + | Ex.<span style="color:black">:</span> Derivatan av <math> \, f(x) = e\,^2 \, </math> är inte <math> \, 2 \, e \, </math> utan <math> \; f\,'(x) = 0 \; </math>, för <math> \, e \, \, = \, 2,718281828\ldots</math> är en konstant och därmed även <math> \, e\,^2 \, </math>. |
| − | |||
| + | <div class="ovnE"> | ||
| + | <small> | ||
| + | ==== Ett försök med derivatans definition ==== | ||
| − | + | Derivatans definition för <math> \, y = f(x) = e\,^x \, </math> leder till<span style="color:black">:</span> | |
| + | :<math> y\,' = \lim_{h \to 0}\,{f(x + h) - f(x) \over h} = \lim_{h \to 0}\,{e\,^{x + h} - e\,^x \over h} = \lim_{h \to 0}\,{e\,^x \cdot e\,^h - e\,^x \over h} = \lim_{h \to 0}\,{e\,^x \, (e\,^h - 1) \over h} = e\,^x \cdot \lim_{h \to 0}\,{e\,^h - 1 \over h} </math> | ||
| − | + | Det är lite svårt för oss att inse att värdet på den sista limes är <math> \, 1 </math>. Detta kan t.ex. visas med den s.k. ''potensserieutvecklingen'' av <math> \, e\,^x </math> <math>-</math> som dock inte ingår i gymnasiematematiken. Så vi kan inte slutföra beviset med derivatans definition. | |
| − | + | Därför väljer vi en annan metod för att bevisa [[2.6_Derivatan_av_exponentialfunktioner#Deriveringsregeln_f.C3.B6r_.5C.28_y_.5C.2C_.3D_.5C.2C_e.5C.2C.5Ex_.5C.29|<b><span style="color:blue">deriveringsregeln </span></b>]] <math> \; y = e\,^x \, \Rightarrow \, y\,' = e\,^x \, </math>. | |
| − | + | ||
| − | :::::{| class="wikitable" | + | ==== Ny bevisidé ==== |
| + | |||
| + | <div style="border:1px solid black; | ||
| + | display:inline-block !important; | ||
| + | margin-left: 10px !important; | ||
| + | padding:10px 20px 10px 20px; | ||
| + | border-radius: 15px;"><b>Kan bland exponentialfunktionerna <math> \; y = b\,^x \; </math> <span style="color:red">basen</span> <math> \, b \, </math> väljas så att derivatan blir samma som funktionen<span style="color:black">:</span> <math> \; y\,' = b\,^x </math> ?</b> | ||
| + | </div> | ||
| + | |||
| + | Istället för att fråga efter derivatan, kräver vi <b><span style="color:red">derivatan = funktionen</span></b> och frågar efter en <b><span style="color:red">bas</span></b> som uppfyller detta krav. | ||
| + | |||
| + | Svaret ges av Eulers bevis nedan. | ||
| + | </small> | ||
| + | </div> | ||
| + | |||
| + | Frågeställningen ovan har i matematikens historia motiverat den schweiziske matematikern [http://sv.wikipedia.org/wiki/Leonhard_Euler <b><span style="color:blue">Leonard Euler</span></b>] att ställa upp sin berömda formel för beräkning av talet <math> \, e \, </math> som redan nämndes i [[1.4 Talet e och den naturliga logaritmen#Hur_kom.28mer.29_talet_.5C.28_e_.5C.2C.5C.29_till.3F|<b><span style="color:blue">Hur kom(mer) talet <math> \, e \,</math> till?</span></b>]] och som vi nu med [[2.3_Gränsvärde|<b><span style="color:blue">limes</span></b>]] kan formulera så här<span style="color:black">:</span> | ||
| + | |||
| + | :::::<math> \lim_{n \to \infty} {\left(1 + {1 \over n}\right)^n} \; =\; e \; = \; 2,718281828\ldots </math> | ||
| + | |||
| + | På 1700-talet bevisade Euler denna formel, varför talet <math> \, e \, </math> kallats efter honom. | ||
| + | |||
| + | <div class="ovnC"> | ||
| + | <small> | ||
| + | ==== Eulers bevis ==== | ||
| + | |||
| + | Vi antar att det finns en bas <math> \,b \, > \, 0 </math> <math>-</math> som än så länge är okänd <math>-</math> så att: | ||
| + | |||
| + | ::<math>\begin{array}{lclcl} y & = & f\,(x) & = & b\,^x \\ | ||
| + | {\color{Red} {y\,'}} & {\color{Red} =} & {\color{Red} {f\,'\,(x)}} & {\color{Red} =} & {\color{Red} {b\,^x}} | ||
| + | \end{array}</math> | ||
| + | |||
| + | I den andra raden har vi formulerat kravet: <b><span style="color:red">derivatan = funktionen</span></b>. | ||
| + | |||
| + | Nu konstruerar vi tangenten till <math> y = b\,^x </math> i punkten <math> \,x = 0 </math>: | ||
| + | |||
| + | Ekvationen för tangenten till kurvan <math> y = b\,^x </math> i punkten <math> \,x = 0 </math> har <math>\,k</math>-formen <math> \; y \, = \, k\,x \, + \, m \; </math> . | ||
| + | |||
| + | Från [[2.4_Derivatans_definition#Resultat:|<b><span style="color:blue">tidigare</span></b>]] vet vi att tangenten till kurvan <math> \, y = b\,^x \, </math> i <math> \, x = 0 \, </math> har en <b><span style="color:red">lutning</span></b> <math>\,k\,</math> som är funktionens <b><span style="color:red">derivata</span></b> i denna punkt. | ||
| + | |||
| + | <table> | ||
| + | <tr> | ||
| + | <td>Derivatan har vi<span style="color:black">:</span> <math> \, {\color{Red} {f\,'(x) = b\,^x}} \, </math> (se ovan). Så vi kan beräkna denna lutning: | ||
| + | |||
| + | ::<math> k \, = \, {\color{Red} {f\,'(0) \, = \, b\,^0}}\, = \, 1 </math> | ||
| + | |||
| + | Tangentens ekvation blir då <math> \, y \, = \, x \, + \, m \, </math> i vilken vi sätter in | ||
| + | |||
| + | tangeringspunktens koordinater <math> \, (0, \, b\,^0) \, = \, (0, 1) \, </math> för att bestämma <math> \, m \, </math>: | ||
| + | |||
| + | ::<math>\begin{array}{rcl} y & = & x \, + \, m \\ | ||
| + | 1 & = & 0 \, + \, m \\ | ||
| + | 1 & = & m | ||
| + | \end{array}</math> | ||
| + | |||
| + | Således blir tangentens ekvation <math> \boxed{\;y \, = \, x \, + \, 1\;} </math> | ||
| + | </td> | ||
| + | <td><math> \quad </math></td> | ||
| + | <td>[[Image: Eulers bevisa.jpg]]</td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | Andra exponentialfunktioner <math> \, y = c\,^x \, </math> med <math> \, c \neq b \, </math> skär denna tangent i två punkter, medan <math> \, y = b\,^x \, </math> med <math> \, y\,' = b\,^x \, </math> tangerar den i punkten <math> \, (0, 1) </math>. | ||
| + | |||
| + | På tangenten <math> \, y = x + 1 \, </math> konstruerar vi en punktföljd <math> P_1, \, P_2, \, P_3, \, \ldots </math> vars <math> \,x</math>-koordinater <math> \, x_n \, </math> bildar talföljden: | ||
| + | |||
| + | ::<math> 1, \, {1 \over 2}, \, {1 \over 3}, \, {1 \over 4}, \, \ldots \quad {\rm med} \quad x_n \, = \, {1 \over n} \quad {\rm som\;allmän \;term,\;där:} \qquad n = 1,\,2,\,3,\,\ldots </math> | ||
| + | |||
| + | Talföljden <math> \,x_n \, </math> ger pga <math> \, y = x + 1 \, </math> upphov till följande talföljd: | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td><math> \,y_n \, = \, x_n + 1 \, = \, {1 \over n} + 1 \, = \, 1 \, + \, {1 \over n} \, </math> på <math> \,y</math>-axeln<span style="color:black">:</span> | ||
| + | |||
| + | <math> \qquad 1\!+\!1, \quad 1\!+\!{1 \over 2}, \quad 1\!+\!{1 \over 3}, \quad 1\!+\!{1 \over 4}, \, \ldots </math> | ||
| + | |||
| + | Punkterna <math> \, P_n = (x_n, \; y_n) = \left({1 \over n}, \; 1 + {1 \over n}\right) \, </math> går mot | ||
| + | |||
| + | tangeringspunkten <math> \, (0, 1) \, </math> när <math> \, n \to \infty </math>. | ||
| + | |||
| + | Punktföljden <math> \, P_n \, </math> ger upphov till en följd av exponen- | ||
| + | |||
| + | tialfunktioner <math> \, y_n = b_n\,^{x_n} \, </math> med vissa baser <math> \, b_n </math>, där<span style="color:black">:</span> | ||
| + | |||
| + | <math> \qquad\qquad b_n \to \, b \quad\; {\rm när} \quad\; n \to \infty </math> | ||
| + | |||
| + | och <math> \, b \, </math> är den efterfrågade basen till <math> \, y = b\,^x \, </math>. | ||
| + | |||
| + | Vi sätter in punktföljdernas allmänna termer <math> \, x_n = {1 \over n} </math> | ||
| + | |||
| + | och <math> \, y_n = 1 + {1 \over n} \, </math> i funktionerna <math> \, y_n = b_n\,^{x_n}\,</math><span style="color:black">:</span> | ||
| + | |||
| + | :::<math>\begin{array}{rcll} y_n & = & b_n\,^{x_n} \\ | ||
| + | \;\; 1 + {1 \over n} & = & b_n\,^{1 \over n} \qquad & | \quad (\,\cdot\,)\,^n | ||
| + | \end{array}</math> | ||
| + | |||
| + | ::<math> \!\boxed{\;\left(1 + {1 \over n}\right)^n \, = \;\; b_n\;} </math> | ||
| + | |||
| + | Nu tar vi <math> \, \displaystyle \lim_{n \to \infty} \, </math> på båda leden för att få Eulers formel: | ||
| + | </td> | ||
| + | <td>[[Image: ExpDeriv2_50a.jpg]]</td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <math> \displaystyle \lim_{n \to \infty} {\left(1 + {1 \over n}\right)^n} \, = \, \lim_{n \to \infty} {b_n} \, = \, b \, </math> som visar sig vara samma tal vars värde vi numeriskt hade fått fram i [[1.4_Talet_e_och_den_naturliga_logaritmen#Hur_kom.28mer.29_talet_.5C.28_e_.5C.2C.5C.29_till.3F|<b><span style="color:blue">Hur kom(mer) talet <math> \, e \,</math> till?</span></b>]] : | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | align=center|<math> n </math> || align=center|<math> 1\,000 </math> || align=center|<math> 1000\,000 </math> || align=center|<math> 1000\,000\,000 </math> || align=center|<math> 10\,000\,000\,000 </math> || align=center|<math> \to \infty </math> | ||
| + | |- | ||
| + | ! align=center| <math> \left(1 + {1 \over n}\right)^n </math> || align=center|<math> {\color{Red} {2,71}}6923932\ldots </math> || <math> {\color{Red} {2,71828}}0469\ldots </math> || align=center|<math> {\color{Red} {2,71828182}}7\ldots </math> || align=center|<math> {\color{Red} {2,718281828\ldots}} </math> || align=center|<math> \quad \to \; {\color{Red} {{\rm Eulers\;tal\;} e}} \quad </math> | ||
| + | |} | ||
| + | |||
| + | Detta demonstrerar att <math> \; \displaystyle \lim_{n \to \infty} {\left(1 + {1 \over n}\right)^n} \, = \, e \; </math> dvs den efterfrågade basen <math> \, b \, </math> är just Eulers tal <math> \, e \, </math>. | ||
| + | </small> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <div class="ovnE"> | ||
| + | <small> | ||
| + | Den inledande frågan i [[2.6_Derivatan_av_exponentialfunktioner#Ny_bevisid.C3.A9|<b><span style="color:blue">Ny bevisidé</span></b>]] kan nu besvaras: | ||
| + | |||
| + | <div style="border:1px solid black; | ||
| + | display:inline-block !important; | ||
| + | margin-left: 10px !important; | ||
| + | padding:10px 20px 10px 20px; | ||
| + | border-radius: 15px;"><b>Kan bland exponentialfunktionerna <math> \; y = b\,^x \; </math> <span style="color:red">basen</span> <math> \, b \, </math> väljas så att derivatan blir samma som funktionen<span style="color:black">:</span> <math> \; y\,' = b\,^x </math> ?</b> | ||
| + | </div> | ||
| + | |||
| + | Svar: | ||
| + | |||
| + | <div style="border:1px solid black; | ||
| + | display:inline-block !important; | ||
| + | margin-left: 10px !important; | ||
| + | padding:10px 20px 10px 20px; | ||
| + | border-radius: 15px;"><b>Ja, det är <span style="color:red">basen</span> <math> \, {\color{Red} {e = }}</math> <span style="color:red">Eulers tal</span> som gör att derivatan av <math> \; y = e\,^x </math> blir samma som funktionen<span style="color:black">:</span> <math> \; {\color{Red} {y\,' = e\,^x}}</math> .</b> | ||
| + | </div> | ||
| + | </small> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | Därför gäller [[2.6_Derivatan_av_exponentialfunktioner#Deriveringsregeln_f.C3.B6r_.5C.28_y_.5C.2C_.3D_.5C.2C_e.5C.2C.5Ex_.5C.29|<b><span style="color:blue">Deriveringsregeln för <math> \, y \,= \,e\,^x \, </math></span></b>]] som ställdes upp inledningsvis. Men: | ||
| + | |||
| + | Hur blir det när konstanter är inblandade? | ||
| + | |||
| + | |||
| + | === <b><span style="color:#931136">Deriveringsregeln för <math> y = C\,e\,^{k\,x} </math></span></b> === | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td><small><div class="border-divblue"> | ||
| + | '''Regel:''' | ||
| + | |||
| + | :<math> \begin{array}{ll} {\rm Derivatan\;av} & y \;\, = \; C\;e\,^{k\,x} \;\; {\rm där} \;\; C,\,k = {\rm const.} \\ | ||
| + | {\rm är} & y\,' = \; C\cdot k\cdot e\,^{k\,x} | ||
| + | \end{array}</math> | ||
| + | |||
| + | Om <math> \, C \, </math>, se [[2.5_Deriveringsregler#Derivatan_av_en_funktion_med_en_konstant_faktor|<b><span style="color:blue">Derivatan av en funktion med en konstant faktor</span></b>]]. | ||
| + | |||
| + | Om <math> \, k \, </math>, se <b><span style="color:red">Kedjeregeln</span></b> i kursen Matematik 4. | ||
| + | </div></small> | ||
| + | |||
| + | |||
| + | |||
| + | </td> | ||
| + | <td><math> \quad </math></td> | ||
| + | <td><small><div class="ovnE"> | ||
| + | '''Exempel 1''' | ||
| + | |||
| + | För funktionen <math> \;\, f(x) \; = \; 2\,e\,^{-\,x} \; </math> blir derivatan: | ||
| + | |||
| + | :::::<math> \;\, f\,'(x) \; = \; 2 \cdot (-1) \cdot e\,^{-\,x} \; = \; -2\,e\,^{-\,x} </math> | ||
| + | |||
| + | '''Exempel 2''' | ||
| + | |||
| + | För funktionen <math> f(x) \; = \; -4\,e\,^{-3\,x} \; </math> blir derivatan: | ||
| + | |||
| + | :::::<math> f\,'(x) \; = \; (-4) \cdot (-3) \cdot e\,^{-3\,x} \; = \; 12\,e\,^{-3\,x} </math> | ||
| + | </div></small> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | |||
| + | Från att ha ställt upp deriveringsregeln för <math> \, y = e\,^x \, </math> går vi nu över till den <b><span style="color:red">allmänna</span></b> exponentialfunktionen <math> \, y = a\,^x \, </math> med godtycklig bas <math> a > 0\, </math>: | ||
| + | |||
| + | === <b><span style="color:#931136">Deriveringsregeln för <math> \, y = a\,^x </math></span></b> === | ||
| + | <div class="border-divblue"> | ||
| + | ::<math> \begin{array}{llcl} {\rm Om} & y & = & a\,^x \;\; {\rm där} \;\; a = {\rm godtycklig\;konstant} \, > \,0 \\ | ||
| + | {\rm då} & y\,' & = & a\,^x \, \cdot \, \ln a | ||
| + | \end{array}</math> | ||
| + | </div> | ||
| + | |||
| + | Specialfallet <math> \, a = e \, </math> och <math> \ln a = \ln e = 1 \, </math> ger derveringsregeln <math> \,y\,' = e^x \, </math> för exponentialfunktionen med basen <math> \, e </math>. | ||
| + | |||
| + | ==== Bevis ==== | ||
| + | |||
| + | Vi börjar med att skriva om basen <math> \, a \, </math> till <math> \,e\,^{\ln a} \, </math>, vilket är möjligt pga inversegenskapen. Då blir det: | ||
| + | |||
| + | :::<math>\begin{array}{rcll} y & = & a\,^x \qquad & : \quad a \, = \,e\,^{\ln a} {\rm \;enligt\;inversegenskapen} \\ | ||
| + | y & = & \left(e\,^{\ln a}\right)^x \qquad & : \quad {\rm 3:e\;potenslagen\;på\;HL} \\ | ||
| + | y & = & e\,^{(\ln a) \, \cdot \, x} \qquad & : \quad \ln a \, = \, k \\ | ||
| + | y & = & e\,^{k \, \cdot \, x} \qquad & | \quad {\rm Derivera\;enligt\;regeln\;ovan} \\ | ||
| + | y\,' & = & k \, \cdot \, e\,^{k\,x} \qquad & : \quad k \, = \, \ln a \\ | ||
| + | y\,' & = & (\ln a) \, \cdot \, e\,^{(\ln a)\,x} \qquad & : \quad {\rm 3:e\;potenslagen\;på\;HL} \\ | ||
| + | y\,' & = & (\ln a) \, \cdot \, \left(e\,^{\ln a}\right)^x \qquad & : \quad e\,^{\ln a} \, = a\, {\rm \;enligt\;inversegenskapen} \\ | ||
| + | y\,' & = & (\ln a) \, \cdot \, a^x \\ | ||
| + | y\,' & = & a^x \, \cdot \, \ln a | ||
| + | \end{array}</math> | ||
| + | |||
| + | |||
| + | Ganska liknande basen <math> \, e \, </math> blir det när konstanter är inblandade i den allmänna exponentialfunktionen <math> \, y = a\,^x \, </math>: | ||
| + | |||
| + | === <b><span style="color:#931136">Deriveringsregeln för <math> y = C\,a\,^{k\,x} </math></span></b> === | ||
| + | |||
| + | <div class="border-divblue"> | ||
| + | Derivatan av exponentialfunktionen <math> y = C\,a\,^{k\,x} </math> med godtycklig bas <math> \, a > 0 </math> och <math> C,\,k = {\rm const.} </math> | ||
| + | |||
| + | ::<math> \begin{array}{llcl} {\rm Om} & y & = & C\,a\,^{k\,x} \;\; {\rm där} \;\; a > 0,\;\; C,\,k = {\rm const.} \\ | ||
| + | {\rm då} & y\,' & = & C\cdot k\cdot a\,^{k\,x} \cdot \ln a | ||
| + | \end{array}</math> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | === <b><span style="color:#931136"> Uppdaterad tabell över deriveringsregler</span></b> === | ||
| + | |||
| + | |||
| + | Vi utvidgar tabellen över deriveringsregler från förra avsnitt med våra nya resultat i detta avsnitt. | ||
| + | |||
| + | I följande tabell är <math> C,\,c,\,k,\,m,\,n,\,a > 0 </math> konstanter medan <math> \boldsymbol{x}\, </math> och <math> \boldsymbol{y}\, </math> är variabler: | ||
| + | |||
| + | <div class="border-divblue"> | ||
| + | {| class="wikitable" | ||
|- | |- | ||
| − | ! <math> y\, </math> || <math> y\,' </math> | + | ! <math> \boldsymbol{y}\, </math> || <math> \boldsymbol{y\,'} </math> |
|- | |- | ||
| align=center| <math> c\, </math> ||align=center| <math> 0\, </math> | | align=center| <math> c\, </math> ||align=center| <math> 0\, </math> | ||
| Rad 59: | Rad 293: | ||
| align=center| <math> x^n\, </math> ||align=center| <math> n\cdot x\,^{n-1} </math> | | align=center| <math> x^n\, </math> ||align=center| <math> n\cdot x\,^{n-1} </math> | ||
|- | |- | ||
| − | | align=center| <math> a\,x\,^n </math> ||align=center| <math> | + | | align=center| <math> a\,x\,^n </math> ||align=center| <math> a\cdot n\cdot x\,^{n-1} </math> |
|- | |- | ||
| − | | align=center| <math> {1 \over x} </math> ||align=center| <math> - {1 \over x^2} </math> | + | | align=center| <math> \displaystyle {1 \over x} </math> ||align=center| <math> \displaystyle - {1 \over x^2} </math> |
|- | |- | ||
| − | | align=center| <math> \sqrt{x} </math> ||align=center| <math> {1 \over 2\, \sqrt{x}} </math> | + | | align=center| <math> \sqrt{x} </math> ||align=center| <math> \displaystyle {1 \over 2\, \sqrt{x}} </math> |
|- | |- | ||
| align=center| <math> e\,^x </math> ||align=center| <math> e\,^x </math> | | align=center| <math> e\,^x </math> ||align=center| <math> e\,^x </math> | ||
| Rad 69: | Rad 303: | ||
| align=center| <math> e\,^{k\,x} </math> ||align=center| <math> k\cdot e\,^{k\,x} </math> | | align=center| <math> e\,^{k\,x} </math> ||align=center| <math> k\cdot e\,^{k\,x} </math> | ||
|- | |- | ||
| − | | align=center| <math> | + | | align=center| <math> C\cdot e\,^{k\,x} </math> ||align=center| <math> C\cdot k\cdot e\,^{k\,x} </math> |
|- | |- | ||
| align=center| <math> a\,^x </math> ||align=center| <math> a\,^x \cdot \ln a </math> | | align=center| <math> a\,^x </math> ||align=center| <math> a\,^x \cdot \ln a </math> | ||
|- | |- | ||
| − | | align=center| <math> | + | | align=center| <math> C\cdot a\,^{k\,x} </math> ||align=center| <math> C\cdot k\cdot a\,^{k\,x} \cdot \ln a </math> |
|- | |- | ||
| align=center| <math> a\cdot f(x) </math> ||align=center| <math> a\cdot f\,'(x) </math> | | align=center| <math> a\cdot f(x) </math> ||align=center| <math> a\cdot f\,'(x) </math> | ||
| + | |- | ||
| + | | align=center| <math> f(x) + g(x)\, </math> ||align=center| <math> f\,'(x) + g\,'(x) </math> | ||
|} | |} | ||
| + | </div> | ||
| − | De två sista raderna i tabellen är snarare generella satser än deriveringsregler. De gäller för alla funktioner <math> f(x)\, </math> och <math> g(x)\, </math>. Av praktiska skäl tar vi upp dem ändå i samma tabell som deriveringsreglerna. | + | De två sista raderna i tabellen är snarare generella satser än deriveringsregler. De gäller för alla funktioner <math> f(x)\, </math> och <math> g(x)\, </math>. Av praktiska skäl tar vi upp dem ändå i samma tabell som deriveringsreglerna. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Denna tabell kommer att kompletteras i Matte 4-kursen då vi kommer att lära oss ytterligare deriveringsregler: regler för derivatan av en produkt resp. kvot av funktioner, den s.k. <b><span style="color:red">Produkt-</span></b> resp. <b><span style="color:red">Kvotregeln</span></b> samt deriveringsregeln för sammansatta funktioner, den s.k. <b><span style="color:red">Kedjeregeln</span></b>. | |
| + | </big> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[Matte:Copyrights|Copyright]] © | + | [[Matte:Copyrights|Copyright]] © 2021 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved. |
Nuvarande version från 7 november 2021 kl. 13.40
| << Förra avsnitt | Genomgång | Övningar | Nästa avsnitt >> |
Målet i detta avsnitt är att ställa upp deriveringsregeln för den allmänna exponentialfunktionen \( \, y = a\,^x \, \) med en godtycklig bas \( a > 0 \).
Detta gör vi genom att först härleda derivatan av exponentialfunktionen \( \, y = e\,^x \, \) med basen \( \, e = \) Eulers tal
och sedan gå över till godtycklig bas \( \,a \). Rpeptera gärna Talet e och den naturliga logaritmen från kap 1 Algebra & funktioner.
Deriveringsregeln för \( y \, = \, e\,^x \)
Derivatan av exponentialfunktionen med basen \( \, e \, \) är funktionen själv:
- \[ \begin{array}{llcl} {\rm Om} & y & = & e\,^x \;\; {\rm där} \;\; e = {\rm Eulers\;tal} \\ {\rm då} & y\,' & = & e\,^x \end{array}\]
OBS! Förväxla denna regel inte med Regeln om derivatan av en potens, därför att:
\( y \, = \, e\,^x \, \) är ingen potens- utan en exponentialfunktion. \( \, x \, \) förekommer i exponenten, inte i basen.
Ex.: Derivatan av \( \, f(x) = e\,^2 \, \) är inte \( \, 2 \, e \, \) utan \( \; f\,'(x) = 0 \; \), för \( \, e \, \, = \, 2,718281828\ldots\) är en konstant och därmed även \( \, e\,^2 \, \).
Ett försök med derivatans definition
Derivatans definition för \( \, y = f(x) = e\,^x \, \) leder till:
\[ y\,' = \lim_{h \to 0}\,{f(x + h) - f(x) \over h} = \lim_{h \to 0}\,{e\,^{x + h} - e\,^x \over h} = \lim_{h \to 0}\,{e\,^x \cdot e\,^h - e\,^x \over h} = \lim_{h \to 0}\,{e\,^x \, (e\,^h - 1) \over h} = e\,^x \cdot \lim_{h \to 0}\,{e\,^h - 1 \over h} \]
Det är lite svårt för oss att inse att värdet på den sista limes är \( \, 1 \). Detta kan t.ex. visas med den s.k. potensserieutvecklingen av \( \, e\,^x \) \(-\) som dock inte ingår i gymnasiematematiken. Så vi kan inte slutföra beviset med derivatans definition.
Därför väljer vi en annan metod för att bevisa deriveringsregeln \( \; y = e\,^x \, \Rightarrow \, y\,' = e\,^x \, \).
Ny bevisidé
Istället för att fråga efter derivatan, kräver vi derivatan = funktionen och frågar efter en bas som uppfyller detta krav.
Svaret ges av Eulers bevis nedan.
Frågeställningen ovan har i matematikens historia motiverat den schweiziske matematikern Leonard Euler att ställa upp sin berömda formel för beräkning av talet \( \, e \, \) som redan nämndes i Hur kom(mer) talet \( \, e \,\) till? och som vi nu med limes kan formulera så här:
- \[ \lim_{n \to \infty} {\left(1 + {1 \over n}\right)^n} \; =\; e \; = \; 2,718281828\ldots \]
På 1700-talet bevisade Euler denna formel, varför talet \( \, e \, \) kallats efter honom.
Eulers bevis
Vi antar att det finns en bas \( \,b \, > \, 0 \) \(-\) som än så länge är okänd \(-\) så att:
- \[\begin{array}{lclcl} y & = & f\,(x) & = & b\,^x \\ {\color{Red} {y\,'}} & {\color{Red} =} & {\color{Red} {f\,'\,(x)}} & {\color{Red} =} & {\color{Red} {b\,^x}} \end{array}\]
I den andra raden har vi formulerat kravet: derivatan = funktionen.
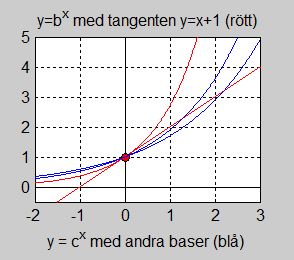
Nu konstruerar vi tangenten till \( y = b\,^x \) i punkten \( \,x = 0 \):
Ekvationen för tangenten till kurvan \( y = b\,^x \) i punkten \( \,x = 0 \) har \(\,k\)-formen \( \; y \, = \, k\,x \, + \, m \; \) .
Från tidigare vet vi att tangenten till kurvan \( \, y = b\,^x \, \) i \( \, x = 0 \, \) har en lutning \(\,k\,\) som är funktionens derivata i denna punkt.
Andra exponentialfunktioner \( \, y = c\,^x \, \) med \( \, c \neq b \, \) skär denna tangent i två punkter, medan \( \, y = b\,^x \, \) med \( \, y\,' = b\,^x \, \) tangerar den i punkten \( \, (0, 1) \).
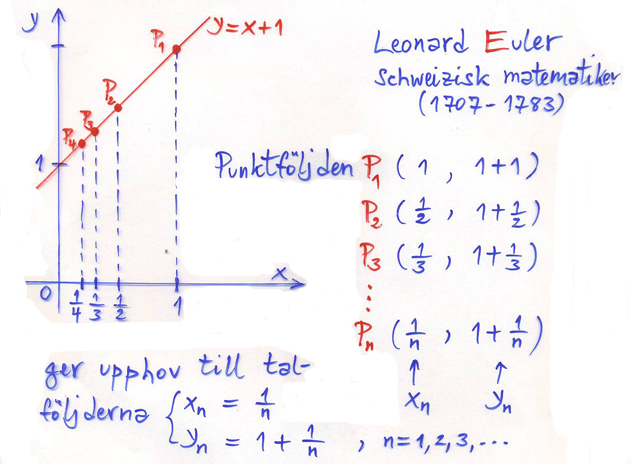
På tangenten \( \, y = x + 1 \, \) konstruerar vi en punktföljd \( P_1, \, P_2, \, P_3, \, \ldots \) vars \( \,x\)-koordinater \( \, x_n \, \) bildar talföljden:
- \[ 1, \, {1 \over 2}, \, {1 \over 3}, \, {1 \over 4}, \, \ldots \quad {\rm med} \quad x_n \, = \, {1 \over n} \quad {\rm som\;allmän \;term,\;där:} \qquad n = 1,\,2,\,3,\,\ldots \]
Talföljden \( \,x_n \, \) ger pga \( \, y = x + 1 \, \) upphov till följande talföljd:
\( \displaystyle \lim_{n \to \infty} {\left(1 + {1 \over n}\right)^n} \, = \, \lim_{n \to \infty} {b_n} \, = \, b \, \) som visar sig vara samma tal vars värde vi numeriskt hade fått fram i Hur kom(mer) talet \( \, e \,\) till? :
| \( n \) | \( 1\,000 \) | \( 1000\,000 \) | \( 1000\,000\,000 \) | \( 10\,000\,000\,000 \) | \( \to \infty \) |
| \( \left(1 + {1 \over n}\right)^n \) | \( {\color{Red} {2,71}}6923932\ldots \) | \( {\color{Red} {2,71828}}0469\ldots \) | \( {\color{Red} {2,71828182}}7\ldots \) | \( {\color{Red} {2,718281828\ldots}} \) | \( \quad \to \; {\color{Red} {{\rm Eulers\;tal\;} e}} \quad \) |
|---|
Detta demonstrerar att \( \; \displaystyle \lim_{n \to \infty} {\left(1 + {1 \over n}\right)^n} \, = \, e \; \) dvs den efterfrågade basen \( \, b \, \) är just Eulers tal \( \, e \, \).
Den inledande frågan i Ny bevisidé kan nu besvaras:
Svar:
Därför gäller Deriveringsregeln för \( \, y \,= \,e\,^x \, \) som ställdes upp inledningsvis. Men:
Hur blir det när konstanter är inblandade?
Deriveringsregeln för \( y = C\,e\,^{k\,x} \)
Regel: \[ \begin{array}{ll} {\rm Derivatan\;av} & y \;\, = \; C\;e\,^{k\,x} \;\; {\rm där} \;\; C,\,k = {\rm const.} \\ {\rm är} & y\,' = \; C\cdot k\cdot e\,^{k\,x} \end{array}\] Om \( \, C \, \), se Derivatan av en funktion med en konstant faktor. Om \( \, k \, \), se Kedjeregeln i kursen Matematik 4.
|
\( \quad \) | Exempel 1 För funktionen \( \;\, f(x) \; = \; 2\,e\,^{-\,x} \; \) blir derivatan:
Exempel 2 För funktionen \( f(x) \; = \; -4\,e\,^{-3\,x} \; \) blir derivatan:
|
Från att ha ställt upp deriveringsregeln för \( \, y = e\,^x \, \) går vi nu över till den allmänna exponentialfunktionen \( \, y = a\,^x \, \) med godtycklig bas \( a > 0\, \):
Deriveringsregeln för \( \, y = a\,^x \)
- \[ \begin{array}{llcl} {\rm Om} & y & = & a\,^x \;\; {\rm där} \;\; a = {\rm godtycklig\;konstant} \, > \,0 \\ {\rm då} & y\,' & = & a\,^x \, \cdot \, \ln a \end{array}\]
Specialfallet \( \, a = e \, \) och \( \ln a = \ln e = 1 \, \) ger derveringsregeln \( \,y\,' = e^x \, \) för exponentialfunktionen med basen \( \, e \).
Bevis
Vi börjar med att skriva om basen \( \, a \, \) till \( \,e\,^{\ln a} \, \), vilket är möjligt pga inversegenskapen. Då blir det:
- \[\begin{array}{rcll} y & = & a\,^x \qquad & : \quad a \, = \,e\,^{\ln a} {\rm \;enligt\;inversegenskapen} \\ y & = & \left(e\,^{\ln a}\right)^x \qquad & : \quad {\rm 3:e\;potenslagen\;på\;HL} \\ y & = & e\,^{(\ln a) \, \cdot \, x} \qquad & : \quad \ln a \, = \, k \\ y & = & e\,^{k \, \cdot \, x} \qquad & | \quad {\rm Derivera\;enligt\;regeln\;ovan} \\ y\,' & = & k \, \cdot \, e\,^{k\,x} \qquad & : \quad k \, = \, \ln a \\ y\,' & = & (\ln a) \, \cdot \, e\,^{(\ln a)\,x} \qquad & : \quad {\rm 3:e\;potenslagen\;på\;HL} \\ y\,' & = & (\ln a) \, \cdot \, \left(e\,^{\ln a}\right)^x \qquad & : \quad e\,^{\ln a} \, = a\, {\rm \;enligt\;inversegenskapen} \\ y\,' & = & (\ln a) \, \cdot \, a^x \\ y\,' & = & a^x \, \cdot \, \ln a \end{array}\]
Ganska liknande basen \( \, e \, \) blir det när konstanter är inblandade i den allmänna exponentialfunktionen \( \, y = a\,^x \, \):
Deriveringsregeln för \( y = C\,a\,^{k\,x} \)
Derivatan av exponentialfunktionen \( y = C\,a\,^{k\,x} \) med godtycklig bas \( \, a > 0 \) och \( C,\,k = {\rm const.} \)
- \[ \begin{array}{llcl} {\rm Om} & y & = & C\,a\,^{k\,x} \;\; {\rm där} \;\; a > 0,\;\; C,\,k = {\rm const.} \\ {\rm då} & y\,' & = & C\cdot k\cdot a\,^{k\,x} \cdot \ln a \end{array}\]
Uppdaterad tabell över deriveringsregler
Vi utvidgar tabellen över deriveringsregler från förra avsnitt med våra nya resultat i detta avsnitt.
I följande tabell är \( C,\,c,\,k,\,m,\,n,\,a > 0 \) konstanter medan \( \boldsymbol{x}\, \) och \( \boldsymbol{y}\, \) är variabler:
| \( \boldsymbol{y}\, \) | \( \boldsymbol{y\,'} \) |
|---|---|
| \( c\, \) | \( 0\, \) |
| \( x\, \) | \( 1\, \) |
| \( a\; x \) | \( a\, \) |
| \( k\; x \, + \, m \) | \( k\, \) |
| \( x^2\, \) | \( 2\,x \) |
| \( a\,x^2 \) | \( 2\,a\,x \) |
| \( x^n\, \) | \( n\cdot x\,^{n-1} \) |
| \( a\,x\,^n \) | \( a\cdot n\cdot x\,^{n-1} \) |
| \( \displaystyle {1 \over x} \) | \( \displaystyle - {1 \over x^2} \) |
| \( \sqrt{x} \) | \( \displaystyle {1 \over 2\, \sqrt{x}} \) |
| \( e\,^x \) | \( e\,^x \) |
| \( e\,^{k\,x} \) | \( k\cdot e\,^{k\,x} \) |
| \( C\cdot e\,^{k\,x} \) | \( C\cdot k\cdot e\,^{k\,x} \) |
| \( a\,^x \) | \( a\,^x \cdot \ln a \) |
| \( C\cdot a\,^{k\,x} \) | \( C\cdot k\cdot a\,^{k\,x} \cdot \ln a \) |
| \( a\cdot f(x) \) | \( a\cdot f\,'(x) \) |
| \( f(x) + g(x)\, \) | \( f\,'(x) + g\,'(x) \) |
De två sista raderna i tabellen är snarare generella satser än deriveringsregler. De gäller för alla funktioner \( f(x)\, \) och \( g(x)\, \). Av praktiska skäl tar vi upp dem ändå i samma tabell som deriveringsreglerna.
Denna tabell kommer att kompletteras i Matte 4-kursen då vi kommer att lära oss ytterligare deriveringsregler: regler för derivatan av en produkt resp. kvot av funktioner, den s.k. Produkt- resp. Kvotregeln samt deriveringsregeln för sammansatta funktioner, den s.k. Kedjeregeln.
Copyright © 2021 TechPages AB. All Rights Reserved.