Skillnad mellan versioner av "3.4 Övningar till Kurvkonstruktioner"
Taifun (Diskussion | bidrag) m (→Övning 8) |
Taifun (Diskussion | bidrag) m |
||
| Rad 2: | Rad 2: | ||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| − | + | {{Not selected tab|[[3.3 Terasspunkter|<-- Förra avsnitt]]}} | |
| − | + | ||
{{Not selected tab|[[3.4 Kurvkonstruktioner|Genomgång]]}} | {{Not selected tab|[[3.4 Kurvkonstruktioner|Genomgång]]}} | ||
{{Selected tab|[[3.4 Övningar till Kurvkonstruktioner|Övningar]]}} | {{Selected tab|[[3.4 Övningar till Kurvkonstruktioner|Övningar]]}} | ||
| Rad 14: | Rad 13: | ||
| − | <Big><Big><Big><span style="color: | + | <Big><Big><Big><span style="color:#A4A4A4">E-övningar: 1-4</span></Big></Big></Big> |
| − | == | + | <div class="ovnE"> |
| − | < | + | == <b><span style="color:#931136">Övning 1</span></b> == |
Följande graf till en funktion med definitionsmängden <math> \, -6 \leq x \leq 5 -</math> är given: | Följande graf till en funktion med definitionsmängden <math> \, -6 \leq x \leq 5 -</math> är given: | ||
| Rad 32: | Rad 31: | ||
d) Anta att grafen visar en polynomfunktion. Ange polynomets grad. Motivera. | d) Anta att grafen visar en polynomfunktion. Ange polynomets grad. Motivera. | ||
| − | + | {{#NAVCONTENT:Svar 1a|3.4 Svar 1a|Svar 1b|3.4 Svar 1b|Lösning 1b|3.4 Lösning 1b|Svar 1c|3.4 Svar 1c|Svar 1d|3.4 Svar 1d|Lösning 1d|3.4 Lösning 1d}}</div> | |
| − | + | ||
| − | <div class=" | + | <div class="ovnE"> |
| + | == <b><span style="color:#931136">Övning 2</span></b> == | ||
Figuren visar grafen till en funktion med samma förlopp som i övning 1, men med en annan definitionsmängd<span style="color:black">:</span> <math> \, -6 < x < 5 \, </math>. | Figuren visar grafen till en funktion med samma förlopp som i övning 1, men med en annan definitionsmängd<span style="color:black">:</span> <math> \, -6 < x < 5 \, </math>. | ||
| Rad 43: | Rad 43: | ||
Ange funktionens största och minsta värde. | Ange funktionens största och minsta värde. | ||
| − | + | {{#NAVCONTENT:Svar 2|3.4 Svar 2a|Lösning 2|3.4 Lösning 2a}}</div> | |
| + | |||
| − | == | + | <div class="ovnE"> |
| − | < | + | == <b><span style="color:#931136">Övning 3</span></b> == |
Följande funktion är given: | Följande funktion är given: | ||
| Rad 61: | Rad 62: | ||
e) Kontrollera dina resultat genom att rita graferna till <math> \, f(x) \, </math> och <math> \, f\,'(x) \, </math> i olika koordinatsystem. | e) Kontrollera dina resultat genom att rita graferna till <math> \, f(x) \, </math> och <math> \, f\,'(x) \, </math> i olika koordinatsystem. | ||
| − | + | {{#NAVCONTENT:Svar 3a|3.4 Svar 3a|Svar 3b|3.4 Svar 3b|Lösning 3b|3.4 Lösning 3b|Svar 3c|3.4 Svar 3c|Lösning 3c|3.4 Lösning 3c|Svar 3d|3.4 Svar 3d|Lösning 3d|3.4 Lösning 3d|Lösning 3e|3.4 Lösning 3e}}</div> | |
| − | + | ||
| − | <div class=" | + | <div class="ovnE"> |
| + | == <b><span style="color:#931136">Övning 4</span></b> == | ||
Följande funktion är definierad i intervallet <math> \, -1 \leq x \leq 5 \, </math><span style="color:black">:</span> | Följande funktion är definierad i intervallet <math> \, -1 \leq x \leq 5 \, </math><span style="color:black">:</span> | ||
| Rad 79: | Rad 81: | ||
e) Kontrollera dina resultat genom att rita grafen till <math> \, f(x) \, </math>. | e) Kontrollera dina resultat genom att rita grafen till <math> \, f(x) \, </math>. | ||
| − | + | {{#NAVCONTENT:Svar 4a|3.4 Svar 4a|Lösning 4a|3.4 Lösning 4a|Lösning 4b|3.4 Lösning 4b|Svar 4c|3.4 Svar 4c|Lösning 4c|3.4 Lösning 4c|Lösning 4d|3.4 Lösning 4d|Lösning 4e|3.4 Lösning 4e}}</div> | |
| − | |||
| − | = | + | <Big><Big><Big><span style="color:#86B404">C-övningar: 5-6</span></Big></Big></Big> |
| − | <div class=" | + | |
| + | |||
| + | <div class="ovnC"> | ||
| + | == <b><span style="color:#931136">Övning 5</span></b> == | ||
En funktions första, andra och tredje derivata är givna i grafisk form: | En funktions första, andra och tredje derivata är givna i grafisk form: | ||
| Rad 96: | Rad 100: | ||
Motivera din skiss. | Motivera din skiss. | ||
| − | + | {{#NAVCONTENT:Svar 5|3.4 Svar 5|Lösning 5|3.4 Lösning 5}}</div> | |
| + | |||
| − | == | + | <div class="ovnC"> |
| − | < | + | == <b><span style="color:#931136">Övning 6</span></b> == |
Kalle kommer hem från skolan där han skrivit nationella provet i Matte 3 och bl.a. löst följande uppgift: | Kalle kommer hem från skolan där han skrivit nationella provet i Matte 3 och bl.a. löst följande uppgift: | ||
| Rad 134: | Rad 139: | ||
Jennifer kollar Kalles lösning och kommer fram till att man från Kalles teckentabell inte kan dra slutsatsen att <math> \, x \, = \, 0 \, </math> är en terasspunkt. | Jennifer kollar Kalles lösning och kommer fram till att man från Kalles teckentabell inte kan dra slutsatsen att <math> \, x \, = \, 0 \, </math> är en terasspunkt. | ||
| − | Jennifer identifierar <math> \, x \, = \, 0 \, </math> som en annan typ av [[ | + | Jennifer identifierar <math> \, x \, = \, 0 \, </math> som en annan typ av [[Detta avsnitt ingår inte i demon.|<strong><span style="color:blue">kritisk punkt</span></strong>]]. |
a) Vem har rätt? Varför? Lös uppgiften själv. | a) Vem har rätt? Varför? Lös uppgiften själv. | ||
| Rad 142: | Rad 147: | ||
c) Visualisera dina resultat. | c) Visualisera dina resultat. | ||
| − | + | {{#NAVCONTENT:Svar 6a|3.4 Svar 6a|Lösning 6a|3.4 Lösning 6a|Svar 6b|3.4 Svar 6b|Lösning 6b|3.4 Lösning 6b|Lösning 6c|3.4 Lösning 6c}}</div> | |
| − | |||
| − | = | + | <Big><Big><Big><span style="color:#62D9FD">A-övningar: 7-8</span></Big></Big></Big> |
| − | <div class=" | + | |
| + | |||
| + | <div class="ovnA"> | ||
| + | == <b><span style="color:#931136">Övning 7</span></b> == | ||
Ställ upp en 3:e gradsfunktion som går genom origo och har: | Ställ upp en 3:e gradsfunktion som går genom origo och har: | ||
| Rad 160: | Rad 167: | ||
d) Visualisera dina resultat genom att rita graferna till funktionerna ovan samt deras derivator. | d) Visualisera dina resultat genom att rita graferna till funktionerna ovan samt deras derivator. | ||
| − | + | {{#NAVCONTENT:Svar 7a|3.4 Svar 7a|Lösning 7a|3.4 Lösning 7a|Svar 7b|3.4 Svar 7b|Lösning 7b|3.4 Lösning 7b|Svar 7c|3.4 Svar 7c|Lösning 7c|3.4 Lösning 7c|Lösning 7d|3.4 Lösning 7d}}</div> | |
| + | |||
| − | == | + | <div class="ovnA"> |
| − | < | + | == <b><span style="color:#931136">Övning 8</span></b> == |
Följande funktion är given: | Följande funktion är given: | ||
| Rad 181: | Rad 189: | ||
<!-- </div>{{#NAVCONTENT:Svar 8a|3.4 Svar 8a|Lösning 8a|3.4 Lösning 8a|Svar 8b|3.4 Svar 8b|Lösning 8b|3.4 Lösning 8b|Lösning 8c|3.4 Lösning 8c}} --> | <!-- </div>{{#NAVCONTENT:Svar 8a|3.4 Svar 8a|Lösning 8a|3.4 Lösning 8a|Svar 8b|3.4 Svar 8b|Lösning 8b|3.4 Lösning 8b|Lösning 8c|3.4 Lösning 8c}} --> | ||
| − | + | {{#NAVCONTENT:Svar 8a|3.4 Svar 8a|Lösning 8a|Denna lösning ingår inte i demon.|Svar 8b|3.4 Svar 8b|Lösning 8b|Denna lösning ingår inte i demon.|Lösning 8c|3.4 Lösning 8c}}</div> | |
| Rad 190: | Rad 198: | ||
| − | [[Matte:Copyrights|Copyright]] © 2011-2015 | + | [[Matte:Copyrights|Copyright]] © 2011-2015 Math Online Sweden AB. All Rights Reserved. |
Versionen från 3 juli 2015 kl. 13.53
| <-- Förra avsnitt | Genomgång | Övningar | --> Nästa avsnitt |
I alla övningar där det förekommer "Rita grafen ..." ska du använda grafräknaren.
E-övningar: 1-4
Övning 1
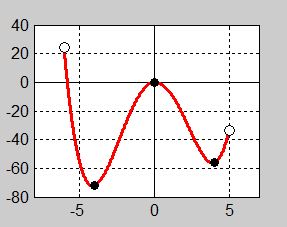
Följande graf till en funktion med definitionsmängden \( \, -6 \leq x \leq 5 -\) är given:
a) Avläs funktionens största och minsta värde.
b) Hur många nollställen har funktionens derivata? Motivera.
c) Avläs derivatans nollställen.
d) Anta att grafen visar en polynomfunktion. Ange polynomets grad. Motivera.
Övning 2
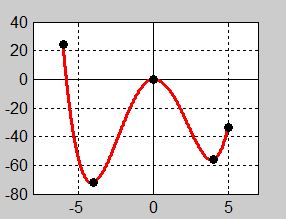
Figuren visar grafen till en funktion med samma förlopp som i övning 1, men med en annan definitionsmängd: \( \, -6 < x < 5 \, \).
Ange funktionens största och minsta värde.
Övning 3
Följande funktion är given:
- \[ f(x) \, = \, {4 \over 3} \, x^3 - 16 \, x \]
a) Derivera \( \, f(x) \, \) två gånger.
b) Beräkna derivatans nollställen.
c) Sätt in derivatans nollställen i andraderivatan och avgör om \( \,f(x) \, \) har några lokala maximi-, minimi- eller terasspunkter.
d) Ange de i c) hittade punkters koordinater.
e) Kontrollera dina resultat genom att rita graferna till \( \, f(x) \, \) och \( \, f\,'(x) \, \) i olika koordinatsystem.
Övning 4
Följande funktion är definierad i intervallet \( \, -1 \leq x \leq 5 \, \):
- \[ y \, = \, f(x) \, = \, -{x^3 \over 3} \, + \, 2\,x^2 \, - \, 3\,x \, + \, 1 \qquad \]
a) Undersök algebraiskt om \( \,f(x) \, \) har några lokala maximi-, minimi- eller terasspunkter och ange deras koordinater.
b) Skissa dina resultat från a).
c) Beräkna funktionens största och minsta värden.
d) Inför dina resultat i samma skiss som i b) och skissa förloppet till \( \, f(x) \, \).
e) Kontrollera dina resultat genom att rita grafen till \( \, f(x) \, \).
C-övningar: 5-6
Övning 5
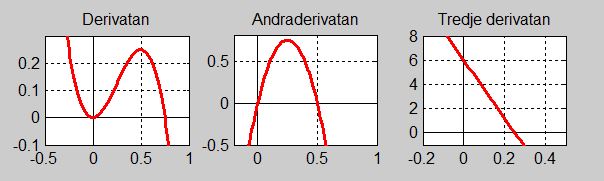
En funktions första, andra och tredje derivata är givna i grafisk form:
Använd graferna ovan för att skissa det ungefärliga förloppet till funktionen \( \, f(x) \, \).
Motivera din skiss.
Övning 6
Kalle kommer hem från skolan där han skrivit nationella provet i Matte 3 och bl.a. löst följande uppgift:
Undersök om följande funktion har en lokal maximi-, minimi- eller terasspunkt för \( \, x \, = \, 0 \, \):
- \[ \, f(x) \, = \, x^4\, (1 \, - \, x) \, \]
Han berättar för Jennifer att han pga följande teckentabell har identifierat \( \, x \, = \, 0 \, \) som en terasspunkt:
| \(x\) | \(-1\) | \(0\) | \(1\) |
| \( f\,'(x) \) | \(-\) | \(0\) | \(-\) |
| \( \,f(x) \) | ↘ | Terass | ↘ |
Dessutom berättar Kalle att han på sin grafräknare har ritat grafen till \( \, f(x) \, \) som även visat en terasspunkt.
Jennifer kollar Kalles lösning och kommer fram till att man från Kalles teckentabell inte kan dra slutsatsen att \( \, x \, = \, 0 \, \) är en terasspunkt.
Jennifer identifierar \( \, x \, = \, 0 \, \) som en annan typ av kritisk punkt.
a) Vem har rätt? Varför? Lös uppgiften själv.
b) Har \( \, f(x) \, \) även andra kritiska punkter? Om ja, hitta och identifiera dem.
c) Visualisera dina resultat.
A-övningar: 7-8
Övning 7
Ställ upp en 3:e gradsfunktion som går genom origo och har:
a) Endast en kritisk punkt.
b) Exakt två kritiska punkter.
c) Ingen kritisk punkt alls.
d) Visualisera dina resultat genom att rita graferna till funktionerna ovan samt deras derivator.
Övning 8
Följande funktion är given:
- \[ f(x) \, = \, x^2 \, (x + 1) \, (2\,x + 5) + 1 \]
a) Bestäm funktionens alla ev. lokala maximi-, minimi- eller terasspunkter och ange deras koordinater.
b) Hitta funktionens alla inflexionspunkter samt deras koordinater.
c) Rita grafen till \( \, f(x) \, \) och \( \, f\,'(x) \, \) i två olika koordinatsystem.
- Markera inflexionspunkterna i båda graferna.
- Förklara varför derivatan har sina extrema i funktionens inflexionspunkter.
Ange alla numeriska svar med tre decimaler.
Copyright © 2011-2015 Math Online Sweden AB. All Rights Reserved.
 Hämtar...
Hämtar...