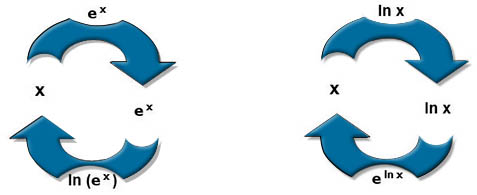Skillnad mellan versioner av "1.4 Talet e och den naturliga logaritmen"

Versionen från 22 september 2015 kl. 11.04

<-- Förra avsnitt

Repetition: Exp. fkt. & logaritmer

Genomgång

Övningar

Nästa avsnitt -->

Lektion 8 Talet \(\,e\) och den naturliga logaritmen

Talet \( e \,\)

Ta fram din miniräknare, leta efter följande funktionsknapp och tryck på den:

\( e^{\,x} \)

Mata in \( 1 \, \) och stäng parentesen. Nu borde det stå \( \; {\bf e} \) ^ \((1) \; \) i displayen.

Tryck på ENTER så får du:

\( 2,718281828\cdots \)

Du har beräknat \( e{\,^1} \,\) eller talet \( {\color{Blue} e} \), en av matematikens mest kända konstanter, Eulers tal.

Talet är kallat efter den schweiziske matematikern Leonard Euler som levde på 1700-talet.

Det var han som ställde upp formler för beräkningen av detta märkliga tal.

Märkligt, därför att \( \, e \,\) inte ett rationellt tal, dvs det kan inte skrivas som ett bråk (kvot mellan två heltal), precis som talen \( \pi,\, \sqrt{2},\, \sqrt{3},\,\cdots \). Sådana tal kallas irrationella. Anledningen till att de inte kan skrivas som kvoter mellan två heltal är att de har oändligt många decimaler utan något som helst mönster som upprepas (period). Detta kan man själv övertyga sig om genom att beskåda de första 5 miljoner decimaler av talet \( e \,\).

Talet \( e \,\) förekommer bl.a. i en formel som enligt många är en av matematikens vackraste, nämligen sambandet mellan heltalet \( 1\, \), de irrationella talen \( e,\;\pi \) och den s.k. imaginära eneheten \( i\, \):

\( e^{\,2\,\pi\,i} \) \( = 1 \)

Ingen fara, vi har inte för avsikt att närmare gå in på denna komplexa formel. Vi nämner den bara för att illustrera betydelsen av talet \( e \,\).

Ytterligare ett tecken på betydelsen av talet \( e \,\) är de otaliga natur- och ekonomiska lagar som formuleras med hjälp av den s.k. exponentialfunktionen \( {\color{Red} {y = e{\,^x}}} \) som i sin tur ger upphov till sin invers, den s.k. naturliga logaritmen \( {\color{Red} {y = \ln x}} \), logaritmen med basen \( e \, - \) ett alternativ till 10-logaritmen med basen 10 som vi använt i Matte 2.

Hur kom(mer) talet \( e \,\) till?

Det enklaste sättet att beräkna talet \( e \,\) är att ta fram din räknare och \( - \) precis som det beskrevs inledningsvis \( - \) beräkna funktionen \( e^{\,x} \):s värde för \( x=1 \, \) dvs beräkna \( e^1\, \) . Om man nöjer sig med detta är det o.k. Men om man vill veta hur värdet kommer till, kan man använda en av de formler Euler har bevisat:

\[ \left(1 + {1 \over x}\right)^x \to e \quad {\rm när} \quad x \to \infty \]

Det betyder: Uttrycket ovan går mot \( e \,\) när \( x\, \) går mot oändligheten (\( \infty \)). Detta innebär att uttrycket närmar sig allt mer talet \( e \,\) ju större värden \( x\, \) antar. Tabellen nedan visar denna process:

\( x\, \)	\( \left(1 + {1 \over x}\right)^x \)
\( 1\,000 \)	\( {\color{Red} {2,71}}6923932\cdots \)
\( 10\,000 \)	\( {\color{Red} {2,718}}145927\cdots \)
\( 100\,000 \)	\( {\color{Red} {2,7182}}68237\cdots \)
\( 1000\,000 \)	\( {\color{Red} {2,71828}}0469\cdots \)
\( 10\,000\,000 \)	\( {\color{Red} {2,718281}}693\cdots \)
\( 100\,000\,000 \)	\( {\color{Red} {2,7182818}}15\cdots \)
\( 1000\,000\,000 \)	\( {\color{Red} {2,71828182}}7\cdots \)
\( 10\,000\,000\,000 \)	\( {\color{Red} {2,718281828}}\cdots \)
\( \infty \)	\( {\color{Red} {{\rm Eulers\;tal\;} e}} \)

De korrekta siffrorna är rödmarkerade och visar hur uttrycket sakta men säkert konvergerar mot det värde du fick fram i räknaren när du slog in \( e^{\,1} \, \). Så i fortsättningen när vi räknar med talet \( e \,\) nöjer vi oss med följande närmevärde med nio decimaler:

\( e \; = \; 2,718281828\cdots \)

Repetera ina kunskaper från Matte 2 om exponentialfunktioner och logaritmer samt logaritmlagarna.

I repetitionen har vi pratat om exponentialfunktioner, dvs i pluralis, därför att vi där inte hade ct basen. Det beror på vilken bas man väljer, t.ex. \( y = 2\,^x \) eller \( y = 3\,^x,\;\cdots \) . I detta avsnitt väljer vi Eulers tal \( e \,\) som bas och tittar på \( \, y = e\,^x \).

Exponentialfunktionen med basen \( e \,\)

När matematiker pratar om den exponentialfunktionen (i singularis) utan att specificera basen menar de alltid exponentialfunktionen med basen \( \, e\,\) \(-\) som en slags prototyp för alla exponentialfunktioner.

\( y \; = \; e\,^x \)

med grafen:

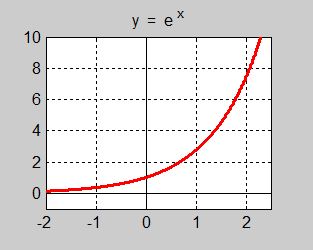
Exponentialfunktionen med basen \( \; {\color{Red} {e = 2,718281828 \ldots}} \)

Några egenskaper hos exponentialfunktionen

Exponentialfunktionen är definierad för alla \( x\, \) och är alltid positiv, dvs \( \, e\,^x \, > \, 0 \, \) för alla \( \, x \). Den blir aldrig \( 0\, \) eller negativ.
\( e\,^0 = 1 \) vilket följer av potenslagarna.
För negativa \( \, x \, \) är \( \, e\,^x < 1 \) och växer allt starkare ju större \( \, x \, \) blir.
Exponentialfunktionen växer starkast bland alla (hittills för oss kända) matematiska funktioner.

Dessa egenskaper menar man när man talar om att en process har exponentiell tillväxt.

Exponentiell tillväxt förekommer både i naturvetenskapliga och ekonomiska tillämpningar. Den har en starkare takt än alla andra tillväxttyper som t.ex. potensfunktioner \( \, x^2 \, \) (kvadratisk) eller \( \, x^3 \, \) (kubisk) osv. Testa gärna genom att rita graferna till potensfunktionerna \( \, y = x^n \, \) för \( \, n = 1, 2, 3, \ldots \, \) och exponentialfunktionen \( \, y = e\,^x \, \) i ett och samma koordinatsystem och jämföra kurvornas branthet.

Att \( \, y \, = \, e\,^x \, \) har en sådan särställning beror på dess betydelse inom den gren av matematiken som vi börjar att studera i nästa kapitel Derivata.

Den naturliga logaritmen

Precis som alla exponentialfunktioner som har sina inversa logaritmfunktioner \(-\) bland dem \( y = 10\,^x\) med inversen \( y = \lg\,x \) \(-\) har även exponentialfunktionen \( y = e\,^x \) med basen \( e\, \) sin inversa logaritmfunktion till basen \( e\, \) dvs \( y = \log_e\,x \). Logaritmen till denna bas kallas den naturliga logaritmen. Och precis som 10-logaritmen har förkortningen \( \lg\, \), har den naturliga logaritmen förkortningen \( \ln\, \) eller LN som står för logaritmus naturalis.

\( y \; = \; \ln x \qquad {\rm logaritmen\;med\;basen} \quad e = 2,718281828\cdots \)

Båda logaritmerna \( \lg\, \) och \( \ln\, \) \(-\) och endast dessa två \(-\) är inprogrammerade i alla (tekniska) kalkylatorer. Däremot har de i räknaren knapparna LOG som står för 10-logaritmen och LN som står för den naturliga logaritmen dvs logaritmen med basen \( e\, \).

Inversegenskapen

Ta fram din miniräknare och beräkna:

\( e^{\,2} \)

Om du inte vet hur det går tryck på den gröna knappen 2nd och sedan på LN vilket ger exponentialfunktionen \( e^{\,x} \). När du ser \( e \, \) ^ \( ( \, \) i displayen, mata in \( 2 \, \), stäng parentesen och tryck på ENTER. Så får du något decimaltal som är \( e^{\,2} \). Låt resultatet stå i displayen.

Fortsätt med att beräkna \( \ln\,(e^{\,2}) \), så här: Tryck på knappen LN, på den gröna knappen 2nd och sedan på knappen (-) vilket ger ANS som står för ANSwer och lagrar räknarens sist beräknade värde, i vårt fall decimaltalet \( e^{\,2} \). Stäng parentesen och tryck på ENTER så får du tillbaka din \( \, 2\):a som du hade matat in i exponentialfunktionen \( e^{\,x} \). Du har beräknat \( \ln\,(e^{\,2}) \) som ger \( \, 2 \):

\( \ln\,(e^{\,2}) \, = \, 2 \)

Med detta experiment \(-\) du kan gärna upprepa det med andra tal \(-\) har du exemplifierat den allmänna inversegenskapen för exponential- och logaritmfunkhionen. De är inversa till varandra (omvända operationer) och tar därför ut varandra. Matematiskt uttryckt innebär detta:

\( \ln\,(e^{\,x}) \, = \, x \qquad {\rm och\; } \qquad e^{\,\ln\,x} \, = \, x \qquad\quad {\rm dvs:\; } e^{\,x} {\rm \;och\; } \ln\,x \;{\rm {\color {Red} {tar\;ut\;varandra}}.} \)

Inversegenskapen gäller alltså oberoende av operationernas ordning: Vare sig du tar först \( e^{\,x} \) och sedan \( \ln\,x \) eller tvärt om, resultatet blir alltid \( \,x \). Dvs man återvänder till det värde \( \,x \) man hade börjat att använda någon av dessa operationer på. Förutsättningen är förstås att man tillämpar \( e^{\,x} \) och \( \ln\,x \) direkt efter varandra.

Både \( \ln\,(e^{\,x}) \) och \( e^{\,\ln\,x} \) är exempel på s.k. sammansatta funktioner. För sådana funktioner gäller regeln: Sammansatta funktioner exekveras (beräknas) inifrån. Ditt eget experiment var ett exempel på detta: Du beräknade först \( e^{\,2} \) och sedan \( \ln\,(e^{\,2}) \).

Så här kan man tänka sig att inversegenskapen för exponential- och logaritmfunkhionen fungerar oberoende av operationernas ordning:

Ekvationen \( e\,^x \, = \, b \)

Fil:Naturliga logaritmen 40.jpg

Egenskaper hos \( y = \ln x \)

Fil:Den naturliga logaritmen.jpg

Några egenskaper hos den naturliga logaritmfunktionen \( y = \ln\,x \) som man kan avläsa från grafen, är:

Logaritmen är definierad endast för positiva \( x\, \). Den är inte definierad för \( x\leq 0\, \).
\( \ln\,1 = 0 \) vilket är logaritmformen till den nollte potensen \( e\,^0 = 1 \).
För \( x < 1\, \) är logaritmen negativ och för \( x > 1\, \) är den positiv.
Logaritmen växer allt svagare ju större \( x\, \) är.

Dessa egenskaper gäller även för logaritmer till andra baser.

Internetlänkar

https://www.youtube.com/watch?v=X-z0aw_q7yM

http://www.youtube.com/watch?v=Z3xsdOvjl4E

http://www.youtube.com/watch?v=_FZJiyqIrG4&feature=related

http://www.youtube.com/watch?v=7RAWXVoyls4

@@ Rad 117: / Rad 117: @@
 <big>
-Exponentiell tillväxt förekommer både i naturvetenskapliga och ekonomiska tillämpningar. Den har en starkare takt än alla andra tillväxttyper som t.ex. potensfunktioner <math> x^2\, </math> (kvadratisk) eller <math> x^3\, </math> (kubisk) osv. Testa gärna genom att rita graferna till potensfunktionerna <math> y = x^n\,</math> för n = 1, 2, 3, ... och exponentialfunktionen <math> y = e\,^x </math> i ett och samma koordinatsystem och jämföra kurvornas branthet.
+Exponentiell tillväxt förekommer både i naturvetenskapliga och ekonomiska tillämpningar. Den har en starkare takt än alla andra tillväxttyper som t.ex. potensfunktioner <math> \, x^2 \, </math> (kvadratisk) eller <math> \, x^3 \, </math> (kubisk) osv. Testa gärna genom att rita graferna till potensfunktionerna <math> \, y = x^n \, </math> för <math> \, n = 1, 2, 3, \ldots \, </math> och exponentialfunktionen <math> \, y = e\,^x \, </math> i ett och samma koordinatsystem och jämföra kurvornas branthet.
 Att <math> \, y \, = \, e\,^x \, </math> har en sådan särställning beror på dess betydelse inom den gren av matematiken som vi börjar att studera i nästa kapitel Derivata.