Skillnad mellan versioner av "1.2 Övningar till Faktorisering av polynom"
Taifun (Diskussion | bidrag) m (→Övning 13) |
Taifun (Diskussion | bidrag) m (→Övning 13) |
||
| Rad 198: | Rad 198: | ||
:::::::<math> x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) </math> | :::::::<math> x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) </math> | ||
| − | <b>Ledning:</b> Sätt in p-q-formeln för <math> x_1\, </math> och <math> x_2\, </math> i högerledet och utveckla produkten där. Använd [[1.1_Fördjupning_till_Polynom#J.C3.A4mf.C3.B6relse_av_koefficienter|<strong><span style="color:blue">jämförelse av koefficienter</span></strong>]] för att visa likheten med vänsterledet. | + | <b>Ledning:</b> Sätt in p-q-formeln för <math> x_1\, </math> och <math> x_2\, </math> i högerledet och utveckla produkten där. |
| + | |||
| + | Använd [[1.1_Fördjupning_till_Polynom#J.C3.A4mf.C3.B6relse_av_koefficienter|<strong><span style="color:blue">jämförelse av koefficienter</span></strong>]] för att visa likheten med vänsterledet. | ||
</div>{{#NAVCONTENT:Lösning 13|1.2 Lösning 13}} | </div>{{#NAVCONTENT:Lösning 13|1.2 Lösning 13}} | ||
Versionen från 28 juni 2014 kl. 11.10
| Repetition Faktorisering | Teori | Övningar | Fördjupning | Internetlänkar |
E-övningar: 1-6
Övning 1
Om
- \[ x^3 - 5\,x^2 + 12\,x - 6 = (x-2) \cdot {\rm (ett\ polynom)} \]
vad är då graden till det okända polynomet?
Övning 2
Vi har:
- \[ 4\,x^2 + 16\,x - 8 = (x+3) \cdot {\rm (ett\ polynom)} \]
a) Vad är graden till det okända polynomet?
b) Vad är koefficienten till x-termen i det okända polynomet?
Övning 3
Ange ett polynom i faktorform vars nollställen är:
a) 2 och 6
b) -2, och -6
c) 1, -5 och 4
Övning 4
Ange nollställen till följande polynom:
a) \( (x-2) \cdot (x+1) \)
b) \( (3\,x-1) \cdot (2\,x+1) \)
Övning 5
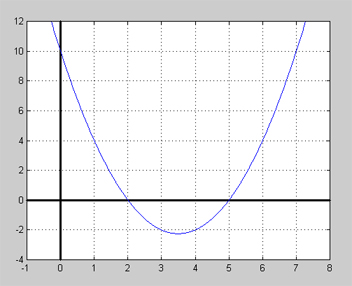
Grafen till en polynomfunktion ser ut så här:
a) Ange några exempel på polynom i faktorform vars nollställen är identiska med kurvans nollställen.
b) Ange det polynom i faktorform vars graf är kurvan ovan.
Övning 6
Faktorisera följande polynom och kontrollera dina svar genom utveckling av de erhållna resultaten:
a) \( x^2 - 6\,x + 8 \)
b) \( 3\,x^2 + 3\,x - 6 \)
c) \( 4\,x^2 - 36 \)
C-övningar: 7-10
Övning 7
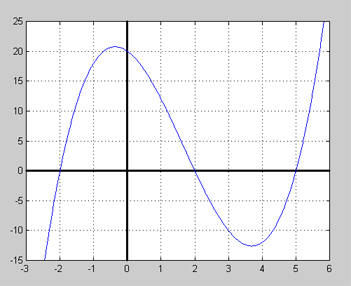
Grafen till en polynomfunktion ser ut så här:
Ange det polynom i faktorform vars graf är kurvan ovan.
Övning 8
Faktorisera följande polynom och kontrollera dina svar genom utveckling av de erhållna resultaten. Ange slutresultaten med heltalskoefficienter.
a) \( 9\,x^2 - 6\,x + 1 \)
b) \( x^2 + 4\,x + 5 \)
c) \( 49\,z^2 + 14\,z + 1 \)
Övning 9
Ange den fullständiga faktoriseringen av polynomet
- \[ x^3 - 9\,x^2 + 26\,x - 24 \]
om en av faktorerna är \( (x-4)\, \).
Övning 10
Vi har följande delfaktorisering av ett 3:e gradspolynom:
- \[ x^3 - 17\,x^2 + 54\,x - 8 = (x-4) \cdot {\rm (ett\ polynom)} \]
a) Bestäm det okända polynomet som en summa av termer.
b) Ange 3:e gradspolynomets fullständiga faktorisering. Svara med två decimaler.
A-övningar: 11-13
Övning 11
Följande 4:e gradspolynom är givet och har dubbelroten \( x = -1\,\):
\[ P(x) = x^4 - 7\,x^3 + 3\,x^2 + 31\,x + 20 \]
a) Ange med hjälp av dubbelroten en delfaktorisering av \( P(x)\,\).
b) Faktorisera \( P(x)\,\) fullständigt.
Övning 12
Anta att två nollställen till polynomet:
\[ P(x) = x^4 + 3\,x^3 - 7\,x^2 - 27\,x - 18 \]
har samma absolutbelopp, men olika förtecken.
a) Bestäm dessa två nollställen och ange en delfaktorisering av \( P(x)\,\).
b) Faktorisera \( P(x)\,\) fullständigt.
Övning 13
Bevisa satsen om faktorisering med 2 nollställen:
Sats:
- Om 2:gradspolynomet \( x^2 + p\,x + q \) har nollställena \( x_1\, \) och \( x_2\, \) så gäller:
- \[ x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) \]
Ledning: Sätt in p-q-formeln för \( x_1\, \) och \( x_2\, \) i högerledet och utveckla produkten där.
Använd jämförelse av koefficienter för att visa likheten med vänsterledet.
Facit
1)
\( 2\, \)
2a)
\( 1\, \)
2b)
\( 4\, \)
3a)
\( (x-2) \cdot (x-6) \)
3b)
\( (x+2) \cdot (x+6) \)
3c)
\( (x-1) \cdot (x+5) \cdot (x-4) \)
4a)
\(x_1 = 2 \; {\rm och} \; x_2 = -1 \)
4b)
\( x_1 = {1 \over 3} \; {\rm och} \; x_2 = -{1 \over 2} \)
5a)
\( \begin{align} & (x-2) \cdot (x-5) \\ 2 \; & (x-2) \cdot (x-5) \\ 6 \; & (x-2) \cdot (x-5) \\ -8 \; & (x-2) \cdot (x-5) \\ \end{align}\)
5b)
\( (x-2) \cdot (x-5) \)
6a)
\( (x-2) \cdot (x-4) \)
6b)
\( y = 3 \cdot (x-1) \cdot (x+2) \)
6c)
\( y = 4 \cdot (x+3) \cdot (x-3) \)
7)
\( (x+2) \cdot (x-2) \cdot (x-5) \)
8a)
\( (3\,x - 1)^2 \)
8b)
Går ej att faktorisera.
8c)
\( (7\,z + 1)^2 \)
9)
\( (x-4) \cdot (x-2) \cdot (x-3) \)
10a)
\( x^2 - 13\,x + 2 \)
10b)
\( (x-4) \cdot (x-0,16) \cdot (x -12,84) \)
11a)
\( (x+1)^2 \cdot (x^2 - 9\,x + 20) \)
11b)
\( (x+1)^2 \cdot (x-4) \cdot (x - 5) \)
12a)
\( x_1 = 3\, \)
\( x_2 = -3\, \)
\( (x+3) \cdot (x-3) \cdot (x^2 + 3\,x + 2) \)
12b)
\( (x+3) \cdot (x-3) \cdot (x+1) \cdot (x+2) \)
Copyright © 2010-2012 Taifun Alishenas. All Rights Reserved.
 Hämtar...
Hämtar...