1.2 Övningar till Faktorisering av polynom
| Teori | Övningar |
G-övningar: 1-6
Övning 1
Om
- \[ x^3 - 5\,x^2 + 12\,x - 6 = (x-2) \cdot {\rm (ett\ polynom)} \]
vad är då graden till det okända polynomet?
Alternativt:
Övning 2
Vi har:
- \[ 4\,x^2 + 16\,x - 8 = (x+3) \cdot {\rm (ett\ polynom)} \]
a) Vad är graden till det okända polynomet?
b) Vad är koefficienten till x-termen i det okända polynomet?
Alternativt:
- Svar 2a | Lösning 2a | Svar 2b | Lösning 2b
Övning 3
Ange ett polynom i faktorform vars nollställen är:
a) 2 och 6
b) -2, och -6
c) 1, -5 och 4
Alternativt:
- Svar 3a | Lösning 3a | Svar 3b | Lösning 3b | Svar 3c | Lösning 3c
Övning 4
Ange nollställen till följande polynom:
a) \( (x-2) \cdot (x+1) \)
b) \( (3\,x-1) \cdot (2\,x+1) \)
Alternativt:
- Svar 4a | Lösning 4a | Svar 4b | Lösning 4b
Övning 5
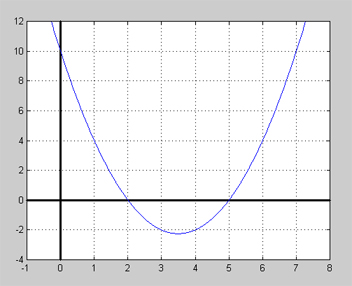
Grafen till en polynomfunktion ser ut så här:
a) Ange några exempel på polynom i faktorform vars nollställen är identiska med kurvans nollställen.
b) Ange det polynom i faktorform vars graf är kurvan ovan.
Alternativt:
Övning 6
Faktorisera följande polynom och kontrollera dina svar genom utveckling av de erhållna resultaten:
a) \( x^2 - 6\,x + 8 \)
b) \( 3\,x^2 + 3\,x - 6 \)
c) \( 4\,x^2 - 36 \)
Alternativt:
- Svar 6a | Lösning 6a | Svar 6b | Lösning 6b | Svar 6c | Lösning 6c
VG-övningar: 7-10
Övning 7
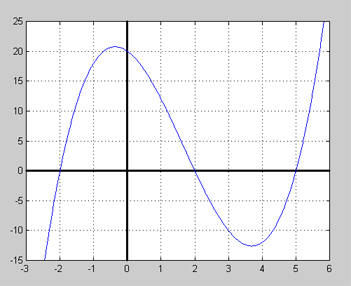
Grafen till en polynomfunktion ser ut så här:
Ange det polynom i faktorform vars graf är kurvan ovan.
Alternativt:
Övning 8
Faktorisera följande polynom och kontrollera dina svar genom utveckling av de erhållna resultaten. Ange slutresultaten med heltalskoefficienter.
a) \( 9\,x^2 - 6\,x + 1 \)
b) \( x^2 + 4\,x - 4 \)
c) \( 49\,z^2 + 14\,z + 1 \)
Alternativt:
- Svar 8a | Lösning 8a | Svar 8b | Lösning 8b | Svar 8c | Lösning 8c
Övning 9
Ange den fullständiga faktoriseringen av polynomet
- \[ x^3 - 9\,x^2 + 26\,x - 24 \]
om en av faktorerna är \( (x-4)\, \).
Alternativt:
Övning 10
Vi har följande delfaktorisering av ett 3:e gradspolynom:
- \[ x^3 - 17\,x^2 + 54\,x - 8 = (x-4) \cdot {\rm (ett\ polynom)} \]
a) Bestäm det okända polynomet som en summa av termer.
b) Ange 3:e gradspolynomets fullständiga faktorisering. Svara med två decimaler.
Alternativt:
MVG-övningar: 11-12
Övning 11
Följande 4:e gradspolynom är givet och har dubbelroten x = -1:
\[ P(x) = x^4 - 7\,x^3 + 3\,x^2 + 31\,x + 20 \]
a) Ange med hjälp av dubbelroten en delfaktorisering av P(x).
b) Faktorisera P(x) fullständigt.
Alternativt:
Övning 12
Anta att två nollställen till polynomet:
\[ P(x) = x^4 + 3\,x^3 - 7\,x^2 - 27\,x - 18 \]
har samma absolutbelopp, men olika förtecken.
a) Bestäm dessa två nollställen och ange en delfaktorisering av P(x).
b) Faktorisera P(x) fullständigt.
Alternativt:
Facit
1)
\( 2\, \)
2a)
\( 1\, \)
2b)
\( 4\, \)
3a)
\( (x-2) \cdot (x-6) \)
3b)
\( (x+2) \cdot (x+6) \)
3c)
\( (x-1) \cdot (x+5) \cdot (x-4) \)
4a)
\(x_1 = 2 \; {\rm och} \; x_2 = -1 \)
4b)
\( x_1 = {1 \over 3} \; {\rm och} \; x_2 = -{1 \over 2} \)
5a)
\( \begin{align} & (x-2) \cdot (x-5) \\ 2 \; & (x-2) \cdot (x-5) \\ 6 \; & (x-2) \cdot (x-5) \\ -8 \; & (x-2) \cdot (x-5) \\ \end{align}\)
5b)
\( (x-2) \cdot (x-5) \)
6a)
\( (x-2) \cdot (x-4) \)
6b)
\( y = 3 \cdot (x-1) \cdot (x+2) \)
6c)
\( y = 4 \cdot (x+3) \cdot (x-3) \)
7)
\( (x+2) \cdot (x-2) \cdot (x-5) \)
8a)
\( (3\,x - 1)^2 \)
8b)
Går ej att faktorisera.
8c)
\( (7\,z + 1)^2 \)
9)
\( (x-4) \cdot (x-2) \cdot (x-3) \)
10a)
\( x^2 - 13\,x + 2 \)
Svar 10b
\( (x-4) \cdot (x-0,16) \cdot (x -12,84) \)
Svar 11a
\( (x+1)^2 \cdot (x^2 - 9\,x + 20) \)
Svar 11b
\( (x+1)^2 \cdot (x-4) \cdot (x - 5) \)
Svar 12a
\( x_1\, = {1 \over 8} \)
\( x_2\, = -1 \)
Svar 12b
\( (x+3) \cdot (x-3) \cdot (x+1) \cdot (x+2) \)
Copyright © 2010-2011 Taifun Alishenas. All Rights Reserved.
 Hämtar...
Hämtar...