3.2 Övningar till Lokala maxima och minima
| <-- Förra avsnitt | Teori | Övningar | --> Nästa avsnitt |
E-övningar: 1-5
Övning 1
| I Introduktion till derivata sysslade vi med följande aktivitet:
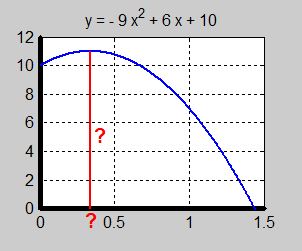
Yulia Koltunova tävlar i simhopp. Hennes hopp från 10-meterstorn beskrivs av funktionen:
där \( {\color{White} x} \; y\, \) är Yulias höjd över vattnet (i meter) och \( {\color{White} {xxxx}} x\, \) är tiden efter hon lämnat brädan (i sekunder). Vi byter frågeställning och vill nu få reda på följande: a) Efter hur många sekunder har Yulia nått sin högsta höjd?
b) Beräkna med hjälp av derivatan Yulias maximala höjd. |
|
Hämtar...Övning 2
a) Följande teckentabell innehåller information om funktionen \(\, y = f(x)\):
| \(x\) | \(-1\) | \(0\) | |||
| \( f\,'(x) \) | \( - \) | \(0\) | \( + \) | \(0\) | \( - \) |
| \( f(x) \) | ↘ | ? | ↗ | ? | ↘ |
- Fyll i tabellen på de platser där det står ett frågetecken (?).
b) Lös övning 1, men använd här en teckentabell för att visa att du hittat maximipunkten.
Övning 3
En sten kastas i luften och följer en bana som beskrivs av funktionen:
- \[ h(t) = - 4\,t^2 + 80\,t \]
där \( {\color{White} x} \; h\, = \, \) stenens höjd över marken i meter
\( {\color{White} {xxxx}} t\, = \, \) tiden efter kastet i sekunder
a) När når stenen sin högsta höjd?
- Använd efter eget godtycke en av reglerna (andraderivatan eller teckentabell) för att visa att du hittat maximipunkten.
b) Hur högt når stenen?
Övning 4
Följande funktion är definierad genom:
Använd grafen till höger för att lösa uppgifterna a)-d): a) Hur många extrempunkter har \( \,f(x) \, \)? b) För vilka \( \,x \) är funktions derivata \( \, = \, 0 \) ? c) Beskriv derivatans teckenbyte i funktions minimum. d) Beskriv derivatans teckenbyte i funktions maximum. Lös uppgift e) algebraiskt: e) Bestäm koordinaterna till funktionens minimum och maximum. |
|
- Använd efter eget godtycke en av reglerna (andraderivatan eller teckentabell) för att visa att du hittat maximi- resp. minimipunkten.
Övning 5
Följande funktion är given:
- \[ f(x) \, = \, {x^4 \over 4} \, - \, 8\,x^2 \]
a) Ställ upp derivatan.
b) Beräkna derivatan \( \, f\,'(x)\):s nollställen.
c) Avgör med någon av metoderna vi lärt oss, vilka av derivatans nollställen är funktionen \( \, f(x)\):s maxima resp. minima.
d) Rita graferna till funktionen \( \, y = f(x) \, \) och derivatan \( \, y\,' = f\,'(x) \, \) i två olika koordinatsystem. Vilket samband kan konstatera mellan funktionens graf och derivatans graf?
C-övningar: 6-8
Övning 6
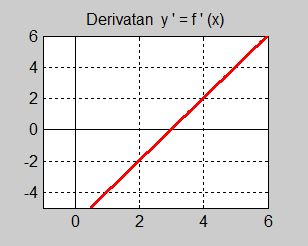
Följande är grafen till derivatan \( {\color{White} x} y' = f'(x) {\color{White} x} \) av en funktion \( \, y = f(x) \, \):
Besvara följande frågor om funktionen \( \, f(x) \, \) genom att använda information från derivatans graf (ovan):
a) För vilka \( \,x \) är funktionen \( \,f(x) \) växande resp. avtagande?
b) Vad kan man säga om funktionen \( f(x) \, \) i derivatans nollställe?
c) Vilken typ av funktion kan \( f(x) \) vara?
d) Rita en ungefärlig skiss över funktionen \( \, y = f(x)\):s förlopp som inte behöver vara en exakt graf.
Övning 7
Följande funktion är given:
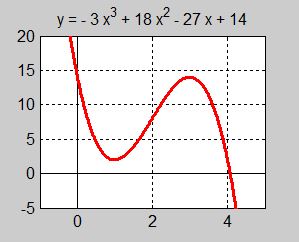
- \[ y = f(x) = -3\,x^3 + 27\,x^2 - 45\,x \]
a) Beräkna derivatans nollställen.
b) Genomför ett teckenstudium och ange med hjälp av en teckentabell för vilka \( \,x \) funktionen \( \,f(x) \) är växande resp. avtagande.
c) Rita grafen till funktionens derivata \( \, y' = f'(x) \).
Ange och motivera endast med hjälp av derivatans graf för vilka \( \,x \) funktionen \( \,f(x) \) är växande resp. avtagande.
Övning 8
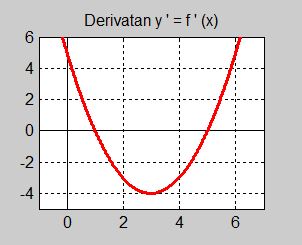
Följande är grafen till derivatan \( {\color{White} x} y' = f'(x) {\color{White} x} \) av en funktion \( \, y = f(x) \, \):
Besvara följande frågor om funktionen \( \, f(x) \, \) genom att använda information från derivatans graf (ovan):
a) Ange för vilka \( \,x \) funktionen \( \,f(x) \) är växande resp. avtagande?
b) Vad händer med funktionen \( f(x) \, \) i de punkter där derivatan är \( \, 0 \, \)?
c) Vilken typ av funktion kan \( f(x) \) vara?
d) Skissa funktionen \( \, y = f(x)\) ungefär.
A-övningar: 9-11
Övning 9
Följande funktion är given:
- \[ f(x) \, = \, x^3 \]
a) Formulera medelvärdessatsen för \( f(x)\, \) i intervallet \( 1 \leq x \leq 3 \). Ange derivatans medelvärde i intervallet \( \, 1 \leq x \leq 3 \, \).
b) Bestäm värdet på \( \, c \, \) så att \( \, f'(c) = \) derivatans medelvärde. Ange svaret med 6 decimaler.
c) Ställ upp ekvationen för tangenten till kurvan \( \, y = x^3 \, \) i punkten \( \, x = c \, \).
d) Ställ upp ekvationen för sekanten genom punkterna \( \, (1, f(1)) \, \) och \( \, (3, f(3)) \, \).
e) Rita graferna till \( \, y = x^3 \, \), tangenten och sekanten i samma koordinatsystem. Tolka resultatet.
Övning 10
I Exempel 2 Oljetank behandlades följande problem:
En oljetank läcker genom ett hål i tankens botten. Utströmningen av oljan beskrivs av funktionen:
- \[ y \, = \, f(x) = \, 4\,x^2 - 380\,x + 9\,000 \]
där \( {\color{White} x} \quad \! x \, = \, {\rm tiden\;i\;minuter} \)
- \[ y \, = \, {\rm oljans\;volym\;i\;liter} \]
Bestäm med hjälp av medelvärdessatsen den tidpunkt då oljetankens utströmningshastighet antar sitt medelvärde i tidsintervallet \( 0 \leq x \leq 45 \). Ange detta medelvärde med hjälp av derivatan och jämför resultatet med Exempel 2 Oljetank b).
Övning 11
I Exempel 1 Vinternatt studerade vi temperaturen som under en vinternatt varierade enligt följande funktion:
- \[ y \, = \, f(x) \, = \, 0,24\,x^2\,-\,2,4\,x\,+\,7 \]
där \( {\color{White} x} \quad \! x \, = \, {\rm tiden\;i\;timmar\;efter\;midnatt} \)
- \[ y \, = \, {\rm temperaturen\;i\;grader\;Celsius} \]
a) Bestäm med hjälp av medelvärdessatsen klockslaget \( \, c \, \) då nattens temperatur ändras i samma takt som temperaturändringens medelvärde mellan kl 1 och kl 6. Ange detta medelvärde. Tolka dina resultat.
b) Visualisera dina resultat genom att rita graferna till \( \, y = f(x) \, \), tangenten till denna kurva i punkten \( \, x = c \, \) och sekanten genom punkterna \( \, (1, f(1)) \, \) och \( \, (6, f(6)) \, \) i samma koordinatsystem. Ange även ekvationerna till tangenten och sekanten.
